P14282 [ICPC 2025 WF] Bride of Pipe Stream

故事仍在继续！几年来，你们的小镇一直有大量 Flubber ——这种可爱但略带易燃性、毒性、酸性、感知力和恶作剧倾向的人造化学物质。人们仍在继续寻找这种物质的更多（或者说，任何）用途。但与此同时， Flubber 工厂继续全力生产。关闭工厂的行动失败了，部分原因是没人知道到底是谁在运营这家工厂。 你被委以重任，要将源源不断的 Flubber 储存到各个 Flubber 储罐中供未来使用（或者，至少让这东西远离大家的头发——字面意思）。为此，你可以使用一个复杂的 Flubber 管道网络，这个网络连接着各个 Flubber 站点和储罐。 每个 Flubber 站点都有一个或多个 Flubber 管道从中引出，并有各种可以升降的闸门，使得流入的 Flubber 能够以任意所需比例排入输出管道。例如，你可以将所有 Flubber 送入一个管道，或者按 `25-75` 的比例分流到两个管道，等等。 相比之下， Flubber 管道向下流向一个或多个较低站点或储罐，但 Flubber 以你无法控制的固定比例排入这些目的地。可能部分 Flubber 会流失到环境中，但那是你的继任者要解决的问题，不是你要解决的问题。 你希望尽快填满所有储罐。也就是说，在所有可能的站点排放配置中，你想要最大化任意储罐中 Flubber 流量的最小值。 图 C.1 展示了两个样例输入。站点和储罐显示为编号节点，初始站点为绿色，储罐为蓝色。其余站点被描绘为白色节点。例如，在第一个样例输入（左侧）中，可以从站点1以任意比例将 Flubber 送入其两个下游管道，但其他管道将根据其出边上打印的百分比分配其流入量。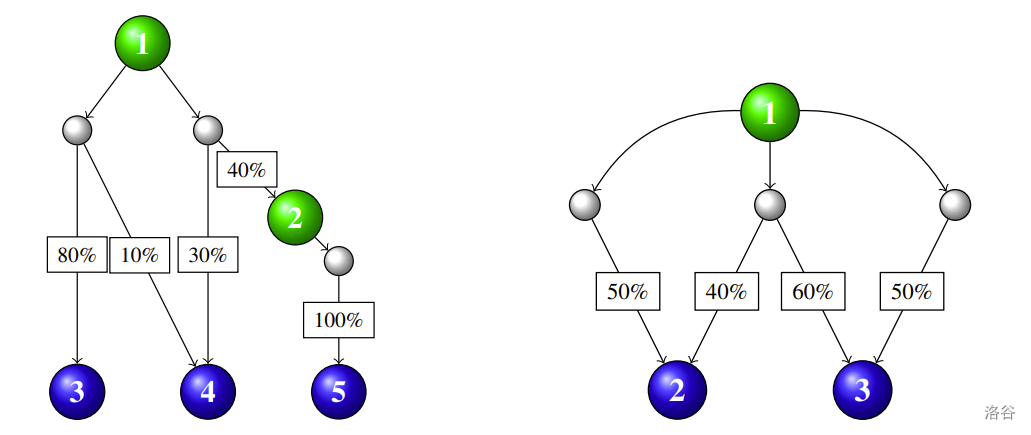  图 C.1：两个样例输入的示意图。

第一行输入包含三个整数 $ s $ 、 $ r $ 和 $ d $ ，其中 $ s $ （$ 1 \le s \le 10\,000 $）是站点数量，$ r $（$ 1 \le r \le 3 $）是储罐数量，$ d $ （$ s \le d \le 20\,000 $）是管道数量。站点编号从 1 到 $ s $ ，储罐编号从 $ s+1 $ 到 $ s+r $ ，按海拔递减顺序排列。工厂的 Flubber 最初流入站点 1 。 接下来的 $ d $ 行每行以两个整数 $ i $ 和 $ n $ 开始，其中 $ i $（$ 1 \le i \le s $）是可以排入此管道的站点，$ n $（$ 1 \le n \le 10 $）是此管道的输出数量。该行剩余部分包含 $ n $ 对整数 $ o $ 和 $ p $ ，其中 $ o $（$ i < o \le s + r $）是此管道排向的站点或储罐，$ p $（$ 1 \le p \le 100 $）是进入管道的 Flubber 将排向 $ o $ 的百分比。给定管道的 $ o $ 值是互不相同的。每个站点至少有一个可以排放的管道。给定管道输出的百分比总和不超过 `100` 。

输出一个数 $ f $ ，表示可能达到的最高百分比，使得在某种站点排放配置下，所有储罐至少接收到工厂生产的 Flubber 的 $ f\% $ 。你的答案的绝对误差应不超过 $ 10^{-6} $ 。