P14285 [ICPC 2025 WF] Herding Cats

You are opening a cat cafe in Baku and would like to take a promotional photograph of all the cats sitting in the front window. Unfortunately, getting cats to do what you want is a famously hard problem. But you have a plan: you have bought a collection of $ m $ catnip plants, each of a different variety, knowing that each cat likes some of these varieties. There is a row of $ m $ pots in the window, numbered 1 to $ m $ in order, and you will place one plant in each pot. Each cat will then be persuaded (by means of a toy on a string) to walk along the row of pots from 1 to $ m $. As soon as a cat reaches a pot with a catnip plant that it likes, it will stop there, even if there already are other cats at that plant. 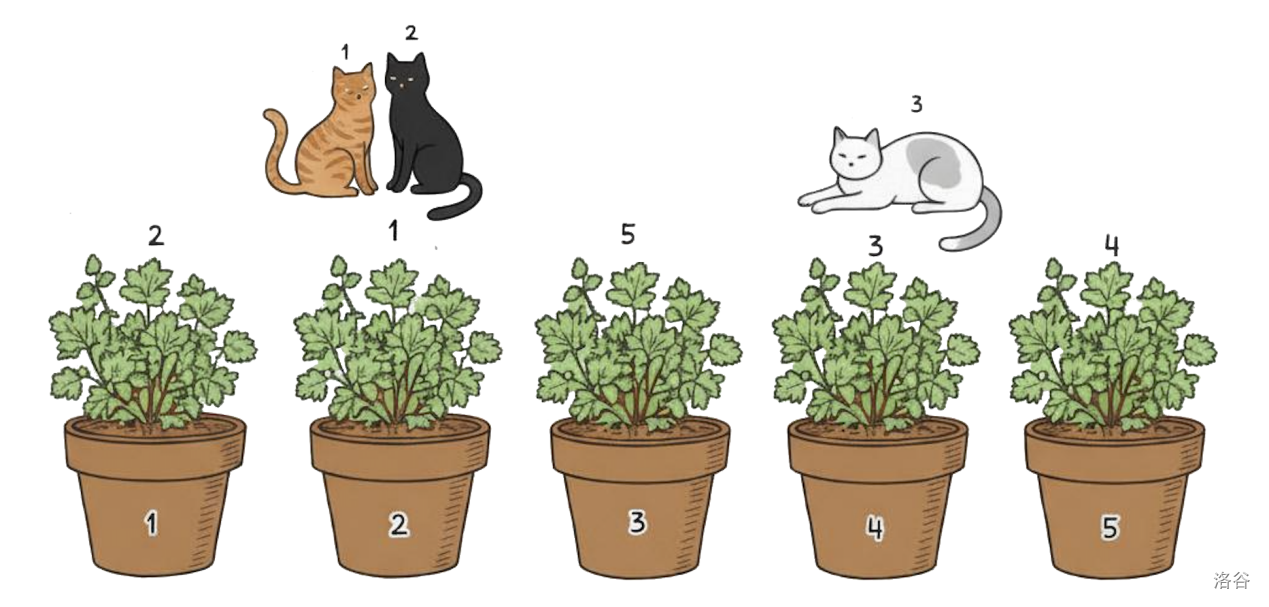:::align{center}  Figure F.1: One possible plant ordering for the first sample test case. ::: You know which pot you would like each cat to stop beside. Can you find a way in which to place the plants in the pots to achieve this?

The first line of input contains an integer $ t $ ($ 1 \le t \le 10\,000 $), which is the number of test cases. The descriptions of $ t $ test cases follow. The first line of each test case contains two integers $ n $ and $ m $, where $ n $ ($ 1 \le n \le 2 \cdot 10^5 $) is the number of cats, and $ m $ ($ 1 \le m \le 2 \cdot 10^5 $) is the number of catnip plants (and also the number of pots). Catnip plants are numbered from 1 to $ m $. The following $ n $ lines each describe one cat. The line starts with two integers $ p $ and $ k $, where $ p $ ($ 1 \le p \le m $) is the pot at which the cat should stop, and $ k $ ($ 1 \le k \le m $) is the number of catnip plants the cat likes. The remainder of the line contains $ k $ distinct integers, which are the numbers of the plants that the cat likes. Over all test cases, the sum of $ n $ is at most $ 2 \cdot 10^5 $, the sum of $ m $ is at most $ 2 \cdot 10^5 $, and the sum of all $ k $ is at most $ 5 \cdot 10^5 $.

For each test case, output either `yes` if it is possible to arrange the catnip plants as described above, or `no` if not.

**Explanation of Sample 1:** In the first test case, a possible ordering of the plants is $[2, 1, 5, 3, 4]$. This way, cat 1 will stop at pot 2, as it is the first pot with a plant variety that it likes. Cat 2 will stop there as well. Cat 3 will continue all the way to pot 4, as shown in Figure F.1.