P14289 [ICPC 2025 WF] Stacking Cups【暂无 spj】

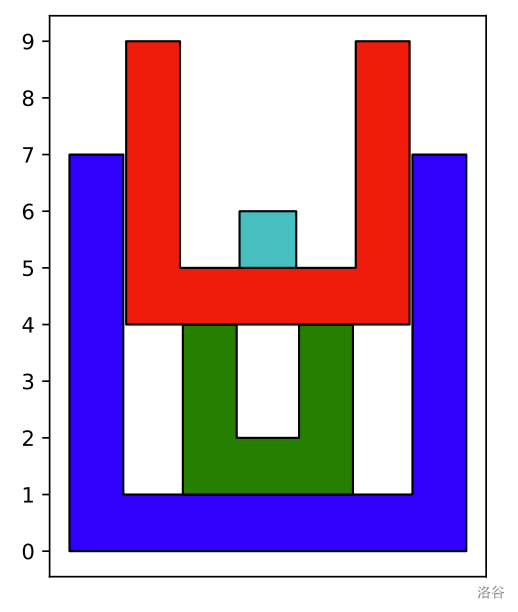
你有 $n$ 个圆柱形杯子，第 $i$ 个杯子的高度为 $2i - 1$ 厘米。这些杯子直径递增，使得杯子 $i$ 能够套在杯子 $j$ 里面，当且仅当 $i < j$。每个杯子的杯底厚度为 $1$ 厘米（这使得最小的杯子只有 $1$ 厘米高，几乎毫无用处，但你还是因为情感原因保留了它）。 在清洗所有杯子后，你会把它们依次叠成一座高塔。每个杯子都正立放置（即开口朝上），且所有杯子的中心线垂直对齐。高塔的高度被定义为所有杯子中最低点到最高点之间的垂直距离。你想知道，应该以怎样的顺序叠放这些杯子，才能使最终的塔高等于你最喜欢的数字。注意，所有 $n$ 个杯子都必须使用。 例如，假设 $n = 4$ 且你最喜欢的数字是 $9$。如果你按高度为 $7,3,5,1$ 的顺序放置这些杯子，如下图所示，最终塔的总高度为 $9$。 :::align{center}  图 J.1：对应样例输出 $1$ 的示意图。 :::

输入包含一行，包括两个整数 $n$ 和 $h$，分别表示杯子的数量和你最喜欢的数字 $h$。$1 \leq n \leq 2 \times 10^5$，$1 \leq h \leq 4 \times 10^{10}$。

如果能够叠出高度为 $h$ 的高塔，输出所有杯子的高度，按照所需的放置顺序输出，以实现该高度。如果不存在这样的顺序，输出 impossible。如果有多种不同的有效放置顺序，输出任意一种都可以。

由 ChatGPT 5 翻译