P14290 [ICPC 2025 WF] Treasure Map

经过多年的寻找，你终于发现了海盗 Blackbeard 的老藏宝图，显示了他那失落已久的宝藏，深藏在海底之下。这张地图曾是一张等高线图——也就是说，它展示了宝藏附近地区的海洋深度——但许多高程标记已随着时间流逝而褪色，现在无法辨认。 具体来说，地图覆盖了一个矩形海域，被细分成 $(n-1) \times (m-1)$ 的单位正方形网格。原本，地图上每个整点 $p=(x, y)$，其中 $1 \leq x \leq n$ 且 $1 \leq y \leq m$，都会标记海洋深度 $d(p)$。已知该区域没有岛屿，也就是说对所有点都有 $d(p) \geq 0$。 绘制这张地图对 Blackbeard 来说必定很具挑战性，因为对于非整点坐标的深度插值，没有唯一自然的方式。考虑位于网格上的一个单位正方形，其四个顶点依次为 $A$、$B$、$C$、$D$（顺时针），每个点 $p \in \{A, B, C, D\}$ 存储一个深度 $d(p)$。一种自然的插值方法是，在三角形 $ABC$ 内进行线性插值，三角形 $CDA$ 也如此。另一种同样自然的方式，是分别在 $BCD$ 和 $DAB$ 内线性插值。通常，这两种插值的结果会不同。例如，如果 $d(A) = d(B) = d(C) = 0$ 且 $d(D) = 1$，第一种方式会使 $ABC$ 区域内的深度始终为零（见下图左），而第二种方式会使该正方形内部所有点的深度为正（见下图右）。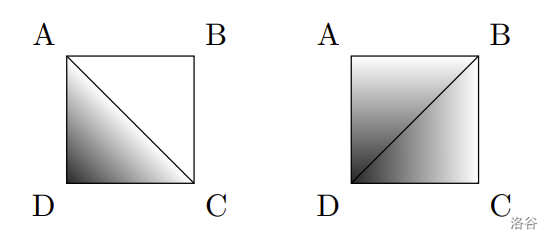 :::align{center}  ::: 然而，Blackbeard 的固执与残忍一样著名，他并不会让这种令人头疼的歧义阻止自己。为了找到藏匿宝藏的绝佳地点，他不惜踏遍七海，寻找海底区域使上述两种插值方法对每个单位正方形来说均得到相同的结果（或者说，他强令手下海盗对海底进行了些“地形改造”——学者们对此说法尚有争议）。 回到现实，现在你正准备组织考察队去打捞宝藏，希望能推断出宝藏可能被埋藏的最浅深度。具体来说，给定藏宝图上依然可辨的部分深度数据，请你计算在宝藏所在位置，可能的最小深度。

第一行输入五个整数 $n$、$m$、$k$、$t_x$ 和 $t_y$，其中 $n$ 和 $m$（$2 \leq n, m \leq 3 \cdot 10^5$）表示网格的最大坐标，$k$（$1 \leq k \leq 3 \cdot 10^5$） 表示已知的深度点数，$(t_x, t_y)$ 是宝藏所在的坐标（$1 \leq t_x \leq n$，$1 \leq t_y \leq m$）。接下来的 $k$ 行每行三个整数 $x$、$y$、$d$（$1 \leq x \leq n$，$1 \leq y \leq m$，$0 \leq d \leq 10^9$），表示网格上 $(x, y)$ 的深度为 $d$。每个 $(x, y)$ 对应的点在输入中至多出现一次。

如果这些已知数据点可以扩展成一份合法的地图（即对于每一个单位方格，两种插值方法的结果一致，且所有点的深度不小于零），输出一个整数：宝藏位置 $(t_x, t_y)$ 可能的最小深度——可以证明这个深度总为整数。否则输出 impossible。

**样例 5 说明：** 即使输入中已给出 $(2,2)$ 点的深度，但这些数据无法扩展成一份合法的地图，因此正确输出为 impossible。 由 ChatGPT 5 翻译