P14296 [JOI2024 预选赛 R2] 高速公路通行费 / Highway Tolls

JOI 王国由 $N$ 个城市组成，这些城市被编号为 $1$ 至 $N$。JOI 王国内有 $M$ 条单向高速公路，这些高速公路被编号为 $1$ 至 $M$。通过高速公路 $i$（$1 \le i \le M$），可以从城市 $A_i$ 移动到城市 $B_i$，所需时间为 $L_i$。 每次通过高速公路都会产生通行费。高速公路 $i$ 的基本通行费为 $C_i$，但由于 JOI 王国的劳动者厌恶加班，若离开基准时刻 $0$ 的时间越久，通行费就会越高。具体而言，若在时刻 $t$ 从城市 $A_i$ 出发并通过高速公路 $i$，则通行费可表示为 $C_i + K \times |t|$，其中 $|t|$ 表示 $t$ 的绝对值。 你居住在城市 $1$，计划前往朋友居住的城市 $N$。你希望确认是否可能通过高速公路从城市 $1$ 移动到城市 $N$，若可能，则进一步求出通行费总和的最小值。你可以自由选择移动路径和在各城市出发的时间。特别地，允许在负时刻从城市 $1$ 出发，也允许在途中某个城市停留一段时间。 给定高速公路的信息以及常数 $K$，请编写一个程序，判断是否可以通过高速公路从城市 $1$ 移动到城市 $N$，若可以，则求出通行费总和的最小值。 此外，在本题的约束条件下，若可以通过高速公路从城市 $1$ 移动到城市 $N$，则通行费总和的最小值必定为整数。

输入以如下格式给出： $N\ M\ K$ $A_1\ B_1\ L_1\ C_1$ $A_2\ B_2\ L_2\ C_2$ $\vdots$ $A_M\ B_M\ L_M\ C_M$

若无法通过高速公路从城市 $1$ 移动到城市 $N$，则输出 $-1$。若可以，则输出一行整数，表示通行费总和的最小值。

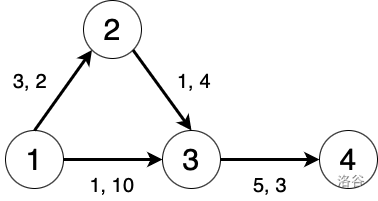
### 样例 1 解释 JOI 王国的城市与道路示意图如下所示。圆圈代表城市，箭头代表道路，每条道路旁标注了其对应的 $L_i$ 和 $C_i$ 的值（按此顺序）。圆圈内标注的数字代表该城市的编号。 :::align{center}  ::: 按以下方式移动时，通行费总和为 15： - 时刻 $-1$：从城市 1 出发，前往城市 3，通行费为 $10 + 2 \times |-1| = 12$。 - 时刻 $0$：到达城市 3，立即前往城市 4，通行费为 $3 + 2 \times |0| = 3$。 - 时刻 $5$：到达城市 4。 不存在通行费总和小于 15 的移动方案，因此输出 15。 该输入样例满足子任务 2、5、6、7 的约束。 ### 样例 2 解释 本样例与样例 1 仅在 $K$ 的取值上不同。 按以下方式移动时，通行费总和为 9： - 时刻 $-3$：从城市 1 出发，前往城市 2，通行费为 $2 + 0 \times |-3| = 2$。 - 时刻 $0$：到达城市 2，立即前往城市 3，通行费为 $4 + 0 \times |0| = 4$。 - 时刻 $1$：到达城市 3，停留于城市 3。 - 时刻 $3$：从城市 3 出发，前往城市 4，通行费为 $3 + 0 \times |3| = 3$。 - 时刻 $8$：到达城市 4。 不存在通行费总和小于 9 的移动方案，因此输出 9。 该输入样例满足子任务 1、2、5、6、7 的约束。 ### 样例 3 解释 无法通过高速公路从城市 1 移动到城市 2，因此输出 $-1$。 该输入样例满足子任务 2、5、6、7 的约束。 ### 样例 5 解释 可能存在多个具有相同 $(A_i, B_i)$ 对的道路。 该输入样例满足子任务 2、4、5、6、7 的约束。 ### 数据范围 - $2 \le N \le 4\,000$。 - $1 \le M \le 8\,000$。 - $0 \le K \le 100\,000$。 - $1 \le A_i \le N$（$1 \le i \le M$）。 - $1 \le B_i \le N$（$1 \le i \le M$）。 - $A_i \ne B_i$（$1 \le i \le M$）。 - $1 \le L_i \le 1\,000\,000$（$1 \le i \le M$）。 - $0 \le C_i \le 10^9$（$1 \le i \le M$）。 - 所有输入的值均为整数。 ### 子任务 1. （9 分）$N \le 100$，$M \le 200$，$K = 0$。 2. （21 分）$N \le 100$，$M \le 200$，$L_i \le 20$（$1 \le i \le M$）。 3. （13 分）$N \le 100$，$M = N - 1$，$A_i = i$，$B_i = i + 1$（$1 \le i \le M$）。 4. （23 分）$N \le 100$，$M \le 200$，并满足以下约束： - $N$ 为偶数，且对所有 $1 \le i \le M$，满足 $\lfloor B_i \div 2 \rfloor - \lfloor A_i \div 2 \rfloor = 1$。其中，$\lfloor x \rfloor$ 表示不超过 $x$ 的最大整数。 5. （16 分）$N \le 100$，$M \le 200$。 6. （11 分）$N \le 1\,500$，$M \le 3\,000$。 7. （7 分）无额外约束。 翻译由 Qwen3-235B 完成。