P14326 [JOI2022 预选赛 R2] 地毯 / Carpet
题目描述
热爱时尚的比太郎新购置了一块地毯。该地毯呈矩形,被划分为 $ H $ 行 $ W $ 列的网格状区域,每个格子被涂成白色或黑色。从上往下第 $ i $ 行、从左往右第 $ j $ 列($ 1 \le i \le H $,$ 1 \le j \le W $)的格子颜色由字符串 $ S_i $ 的第 $ j $ 个字符决定:若为 .,则为白色;若为 #,则为黑色。
比太郎将一枚棋子放置在地毯最左上角的格子上,并设想了一个游戏:通过若干次操作,将棋子移动至地毯最右下角的格子。
- 每次操作,棋子必须移动到与当前所在格子颜色不同的、上下左右相邻的某一格。
比太郎希望尽量减少到达目标所需的步数。但根据地毯的图案,可能根本无法到达目标。
当给出地毯的图案信息时,请编写程序判断:通过重复操作,是否能从左上角格子将棋子移动至右下角格子;若可能,则求出最小操作次数。
输入格式
输入通过标准输入以如下格式给出:
$ H $ $ W $
$ S_1 $
$ S_2 $
$ \vdots $
$ S_H $
输出格式
若通过重复操作可以从左上角格子到达右下角格子,则输出最小操作次数;若无法到达,则输出 $ -1 $。结果请在标准输出中以单行输出。
说明/提示
### 样例 1 解释
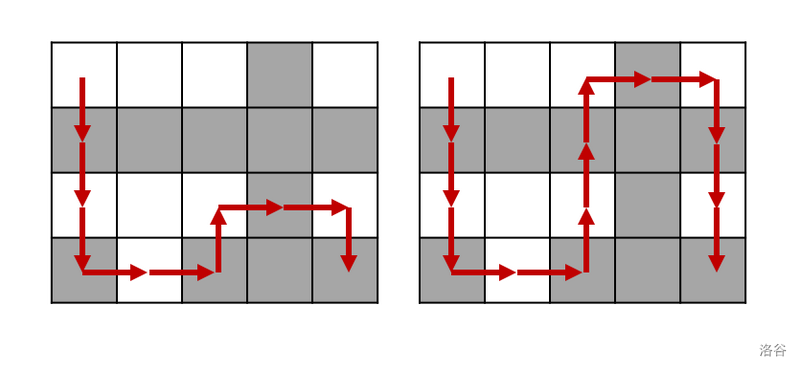
这是符合题目要求的两种走法:
:::align{center}
:::
左侧的走法只需使用 $9$ 次操作就能完成了,右侧的走法需要 $13$ 次操作才能完成。可以证明,不存在小于 $9$ 次操作的方式。
### 数据范围
- $ 1 \le H \le 500 $。
- $ 1 \le W \le 500 $。
- $ (H, W) \ne (1, 1) $。
- $ S_i $ 是长度为 $ W $ 的字符串($ 1 \le i \le H $)。
- $ S_i $ 的每个字符为 . 或 #($ 1 \le i \le H $)。
- $ H $、$ W $ 为整数。
### 子任务
1. (4 分)$ H = 1 $。
2. (14 分)$ H \le 5 $,$ W \le 5 $。
3. (24 分)$ H \le 30 $,$ W \le 30 $。
4. (58 分)无额外约束。
翻译由 Qwen3-235B 完成