P14366 [JOISC 2018] 栅栏 / Fences

JOI 先生在 IOI 国拥有一块很大的土地。IOI 国用一个坐标平面表示，其中 $X$ 轴与 $Y$ 轴互相垂直。坐标为 $x$、$y$ 的点记作 $(x, y)$。他的土地是 $X$ 坐标和 $Y$ 坐标均在 $-10^{100}$ 到 $10^{100}$（含端点）之间的区域。他在一块牧场上饲养奶牛，这块牧场是 $X$ 坐标和 $Y$ 坐标均在 $-S$ 到 $S$（含端点）之间的区域。 JOI 先生决定用一些栅栏围住牧场，以防止奶牛逃出。栅栏由长度为正实数的线段表示。他将围住牧场，使得从牧场内任意一点出发，若不经过任何栅栏（包括栅栏的端点），则无法到达土地的外部。土地上已有一些栅栏，他可以利用这些栅栏来围住牧场。对于这些栅栏中的任意两段，若它们有公共点，则该点必为其中至少一段栅栏的端点。 JOI 先生可以建造任意数量的新栅栏。新栅栏的长度和方向可以任意，只要它不穿过牧场内部或土地外部即可。他也可以建造一段沿着牧场边界的栅栏。建造一段长度为 $l$（$l > 0$）的新栅栏，其成本为 $l$。两段栅栏可能相交，一段栅栏的端点可能与另一段栅栏的端点重合，或一段栅栏的端点可能位于另一段栅栏上。 JOI 先生希望以尽可能低的成本围住牧场。 **任务** 给定牧场的尺寸以及已建栅栏的数据，编写一个程序，计算围住牧场所需的最小总成本。

从标准输入读取以下数据： - 输入的第一行包含两个以空格分隔的整数 $N$ 和 $S$。这意味着牧场是 $X$ 坐标和 $Y$ 坐标均在 $-S$ 到 $S$（含端点）之间的区域，且 JOI 先生的土地上已建有 $N$ 段栅栏。 - 接下来的 $N$ 行中，第 $i$ 行（$1 \le i \le N$）包含四个以空格分隔的整数 $A_i, B_i, C_i, D_i$。这意味着第 $i$ 段已建栅栏是连接点 $(A_i, B_i)$ 与点 $(C_i, D_i)$ 的线段。

向标准输出写入一行。输出应包含围住牧场所需的最小总成本。你可以在小数点后输出任意位数的数字，但你的输出与正确答案之间的绝对误差不得超过 $0.01$。

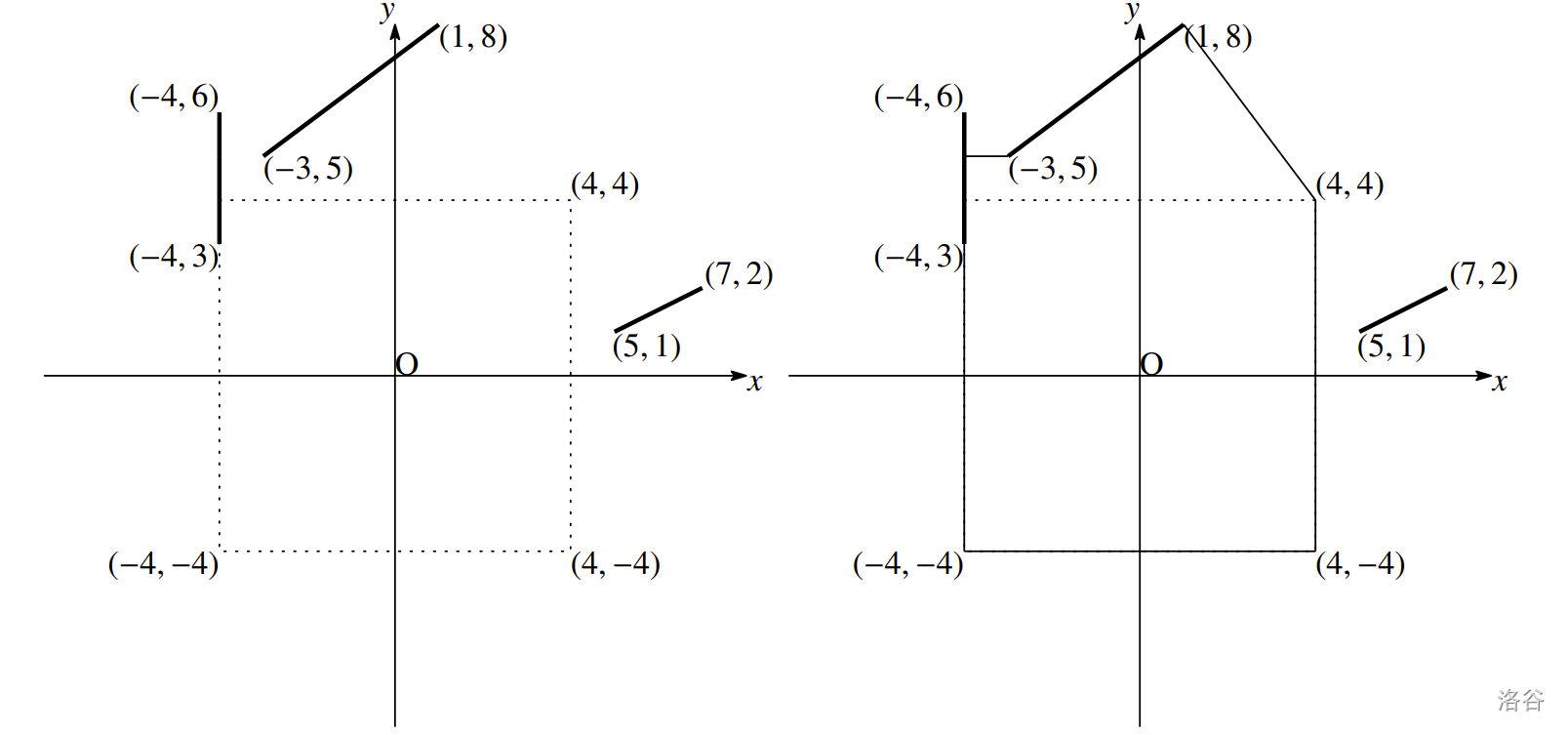
### 样例 1 解释 样例输入 1 中已建的栅栏如下面图片左侧所示。中心的虚线方框表示牧场的边界。 右侧展示了围住该牧场的一种方式，其中细线段代表新建的栅栏。建造这些栅栏的成本为 $29$，这是可能的最小成本。在本样例输入中，除 $29.0000000000$ 外，输出 $29$ 或 $28.999$ 也被视为正确。 :::align{center}  ::: ### 数据范围 所有输入数据满足以下条件： - $1 \le N \le 100$。 - $1 \le S \le 200$。 - $-200 \le A_i \le 200$（$1 \le i \le N$）。 - $-200 \le B_i \le 200$（$1 \le i \le N$）。 - $-200 \le C_i \le 200$（$1 \le i \le N$）。 - $-200 \le D_i \le 200$（$1 \le i \le N$）。 - $(A_i, B_i) \ne (C_i, D_i)$（$1 \le i \le N$）。 - 输入中的任何栅栏都不会严格位于牧场内部。 - 对于输入中任意两个不同的栅栏，若它们有公共点，则该点必为其中至少一个栅栏的端点。 ### 子任务 共有 3 个子任务。每个子任务的得分和附加约束如下： **子任务 1 [18 分]** - $N = 1$。 **子任务 2 [33 分]** - $N \le 6$。 **子任务 3 [49 分]** 无额外约束。 翻译由 Qwen3-235B 完成