P1436 Chessboard Partition

Partition an $8\times 8$ chessboard as follows: cut off a rectangular subboard from the original chessboard so that the remaining part is also a rectangle; then pick either of the two remaining parts and continue to partition it in the same way. After doing this $(n-1)$ times, together with the final remaining rectangle, there are $n$ rectangular boards. 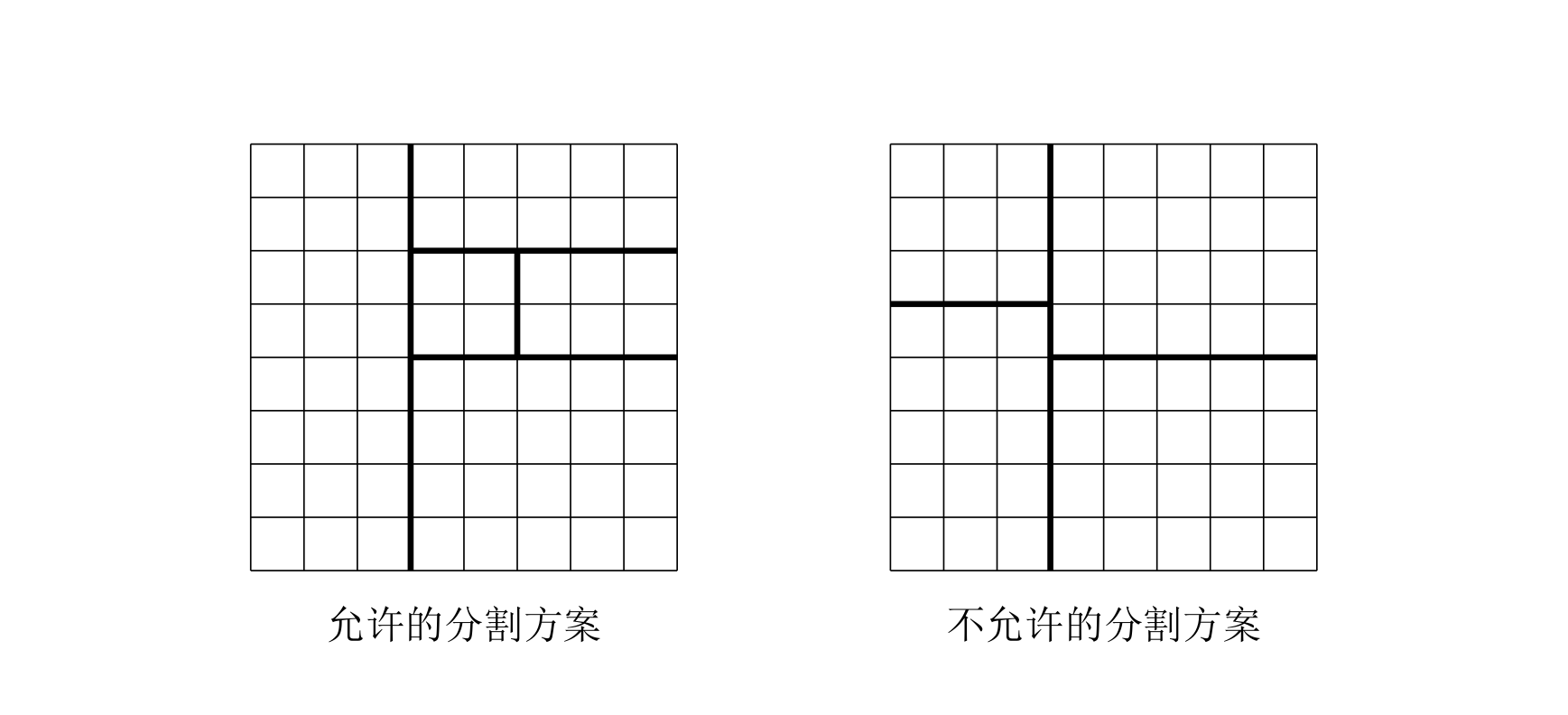(Each cut may only follow the edges of the grid cells.)  Each cell on the original chessboard has a score. The total score of a rectangular board is the sum of the scores of its cells. Partition the chessboard into $n$ rectangles according to the rule above so that the sum of squares of the rectangles’ total scores is minimized. Given the chessboard and $n$, write a program to compute the minimum possible sum of squares.

The first line contains an integer $n\ (1

Output a single number: the minimum sum of squares.

Translated by ChatGPT 5