P14417 [JOISC 2015] 防壁 / Walls
题目描述
你获得了 JOI 社开发的一款电视游戏软件。这是一款相当不错的游戏,你每天都在愉快地游玩。
某天,游戏中出现了一个被称为“**激光**”的关卡。这个关卡极其困难,即使是优秀的玩家也只能以极低的概率通关。在多次挑战这个关卡的过程中,你意识到,如果能做出快速判断,或许就有机会通关,于是你开始思考编写程序来应对这个关卡。
“激光”关卡的舞台是一个设置了 $N$ 个屏障的矩形区域。舞台被划分为 $1 \times 1$ 的正方形格子,每个格子由非负整数 $x, y$ 表示为 $(x, y)$。其中 $(0, 0)$ 是左下角的格子,$(x, y)$ 表示从 $(0, 0)$ 向右移动 $x$ 格、向上移动 $y$ 格到达的格子。
关卡开始时,敌人出现并发动攻击。敌人会连续发动 $M$ 次攻击。第 $j$ 次攻击时,敌人会从格子 $(P_j, N+1)$ 向格子 $(P_j, 0)$ 发射激光。
每个屏障占据若干个 $y$ 坐标相同的格子,形成一个宽度为 $B_i - A_i + 1$、高度为 1 的长方形。屏障 $i$($1 \le i \le N$)在关卡开始时占据从格子 $(A_i, i)$ 到格子 $(B_i, i)$ 的区域。在敌人第一次攻击前,以及每次攻击之间的间隙,你可以随时将任意一个屏障向左或向右移动一格。每次移动只能将一个屏障向右移动一格,或向左移动一格。
激光碰到屏障时威力会减弱。通过移动屏障,使得激光碰到所有屏障,从而将激光的威力降至最低。
你的目标是:在该关卡中,使屏障移动的总次数尽可能少。
### 题目
给定关卡开始时每个屏障的位置,以及每次敌人攻击的位置。当移动屏障使得激光碰到所有屏障时,求每个屏障移动次数的最小值。
输入格式
从标准输入读取以下数据:
- 第一行包含两个整数 $N$ 和 $M$,以空格分隔。这表示该关卡中有 $N$ 个屏障,敌人将发动 $M$ 次攻击。
- 接下来的 $N$ 行中,第 $i$ 行($1 \le i \le N$)包含两个整数 $A_i$ 和 $B_i$,以空格分隔。这表示在关卡开始时,屏障 $i$ 被放置在从格子 $(A_i, i)$ 到格子 $(B_i, i)$ 的位置。
- 接下来的 $M$ 行中,第 $j$ 行($1 \le j \le M$)包含一个整数 $P_j$。这表示在第 $j$ 次攻击时,敌人会从格子 $(P_j, N+1)$ 向格子 $(P_j, 0)$ 立即发射激光。
输出格式
向标准输出输出 $N$ 行。第 $i$ 行($1 \le i \le N$)输出屏障 $i$ 移动次数的最小值。
说明/提示
### 样例 1 解释
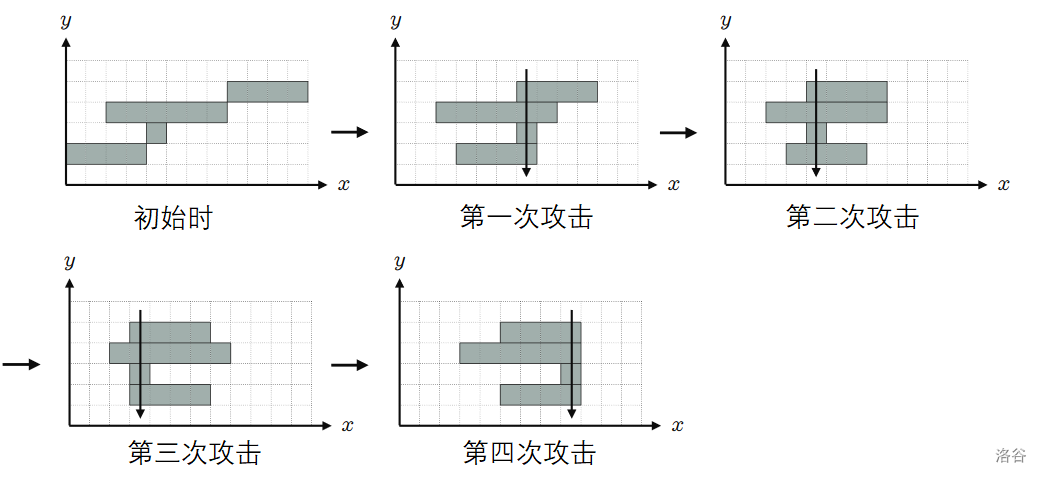
对于该输入,一种使屏障移动次数最小的移动方式如下:
- 在第 1 次攻击前,将屏障 1 向右移动 3 次,屏障 2 向右移动 2 次,屏障 3 保持不动,屏障 4 向左移动 2 次。
- 在第 2 次攻击前,屏障 1 保持不动,屏障 2 向左移动 2 次,屏障 3 保持不动,屏障 4 向左移动 2 次。
- 在第 3 次攻击前,屏障 1 保持不动,屏障 2 向左移动 1 次,屏障 3 保持不动,屏障 4 向左移动 1 次。
- 在第 4 次攻击前,屏障 1 向右移动 2 次,屏障 2 向右移动 5 次,屏障 3 向右移动 1 次,屏障 4 向右移动 2 次。
按照这种移动方式,屏障 1 移动 5 次,屏障 2 移动 10 次,屏障 3 移动 1 次,屏障 4 移动 7 次。
:::align{center}
图片来自于 [LibreOJ](https://loj.ac/p/3006)。
:::
### 数据范围
所有输入数据满足以下条件:
- $1 \le N \le 200000$
- $1 \le M \le 200000$
- $0 \le A_i \le B_i \le 1000000000$($1 \le i \le N$)
- $0 \le P_j \le 1000000000$($1 \le j \le M$)
### 子任务
**子任务 1 [10 分]**
- $N = 1$
**子任务 2 [45 分]**
- $A_i = 0$($1 \le i \le N$)
**子任务 3 [45 分]**
无额外限制。
翻译由 Qwen3-235B 完成