P14422 [JOISC 2014] 水壶 / Water Bottle

翻译来自于 https://loj.ac/p/2876

JOI 君所居住的 IOI 市以一年四季都十分炎热著称。 IOI 市被分成 $H$ 行，每行包含 $W$ 块区域。每个区域都是建筑物、原野、墙壁之一。 IOI 市有 $P$ 个区域是建筑物，坐标分别为 $(A_1,B_1),(A_2,B_2),\dots,(A_P,B_P)$。 JOI 君只能进入建筑物与原野，而且每次只能走到相邻的区域中，且不能移动到市外。 JOI 君因为各种各样的事情，必须在各个建筑物之间往返。虽然建筑物中的冷气设备非常好，但原野上太阳非常毒辣，因此在原野上每走过一个区域都需要 1 升水。此外，原野上没有诸如自动售货机、饮水处之类的东西，因此 IOI 市的市民一般都携带水壶出行。大小为 $x$ 的水壶最多可以装 $x$ 升水，建筑物里有自来水可以将水壶装满。 由于携带大水壶是一件很困难的事情，因此 JOI 君决定携带尽量小的水壶移动。因此，为了随时能在建筑物之间移动，请你帮他写一个程序来计算最少需要多大的水壶。 现在给出 IOI 市的地图和 $Q$ 个询问，第 $i$ 个询问包含两个整数 $S_i,T_i$，对于每个询问，请输出：要从建筑物 $S_i$ 移动到 $T_i$，至少需要多大的水壶？ **题目** 给定 IOI 市的地图及 $Q$ 个查询。第 $i$ 个查询（$1 \le i \le Q$）要求计算“在建筑物 $S_i$ 与 $T_i$ 之间移动所需的最小水壶容量”。请编写程序，对每个查询给出答案。

从标准输入读取以下数据。 - 第一行四个空格分隔的整数 $H,W,P,Q$。 - 接下来 $H$ 行，第 $i$ 行有一个长度为 $W$ 的字符串，每个字符都是 `.` 或 `#` 之一，`.` 表示这个位置是建筑物或原野，`#` 表示这个位置是墙壁。 - 接下来 $P$ 行描述 IOI 市每个建筑物的位置，第 $i$ 行有两个空格分隔的整数 $A_i$ 和 $B_i$ ，表示第 $i$ 个建筑物的位置在第 $A_i$ 行第 $B_i$ 列。保证这个位置在地图中是 `.`。 - 接下来 $Q$ 行，第 $i$ 行有两个空格分隔的整数 $S_i ,T_i$。

输出 $Q$ 行，第 $i$ 行一个整数，表示要从建筑物 $S_i$ 移动到 $T_i$，至少需要多大的水壶。 如果无法到达，输出 `-1`。如果不需要经过原野就能到达，输出 `0`。

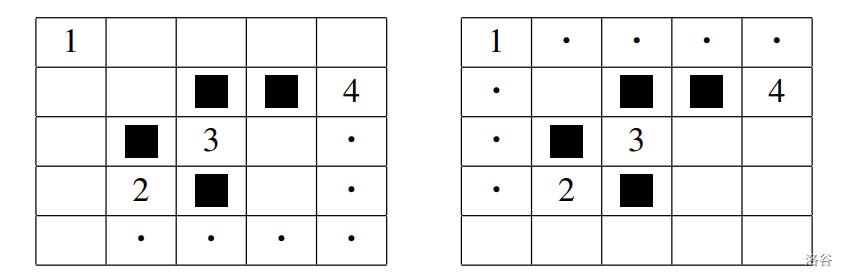
### 样例 1 解释 在此输入中，IOI 市的地图如下图所示。标有黑色方块的格子表示墙壁，标有数字的格子表示对应编号的建筑物，空白格子表示草地。 :::align{center}  ::: 例如，考虑从建筑物 2 移动到建筑物 4。此时，如果不经过其他建筑物，最优的路径是经过左图中用点标出的格子，这样经过的草地格子数最少，需要容量为 $6$ 的水壶。 :::align{center}  ::: 然而，如果像右图所示那样，在移动过程中经过建筑物 1，则从建筑物 2 到建筑物 1 的移动过程中经过 $3$ 个草地格子，从建筑物 1 到建筑物 4 的移动过程中经过 $4$ 个草地格子，因此可以使用容量为 $4$ 的水壶完成移动。此外，无法使用容量小于 $4$ 的水壶完成移动。 ### 数据范围 所有的输入数据满足以下条件： - $1 \leq H \leq 2000$。 - $1 \leq W \leq 2000$。 - $2 \leq P \leq 200\ 000$。 - $1 \leq Q \leq 200\ 000$。 - $1 \leq A_j \leq H$（$1 \leq j \leq P$）。 - $1 \leq B_j \leq W$（$1 \leq j \leq P$）。 - $(A_i, B_i) \neq (A_j, B_j)$（$1 \leq i < j \leq P$）。 - $1 \leq S_i < T_i \leq P$（$1 \leq i \leq Q$）。 ### 子任务 **子任务 1 [10 分]** 满足以下条件： - $H \leq 200$。 - $W \leq 200$。 - $P \leq 200$。 **子任务 2 [30 分]** 满足以下条件： - $P \leq 5\ 000$。 - $Q = 1$。 **子任务 3 [30 分]** 满足以下条件： - $P \leq 5\ 000$。 - $Q \leq 10\ 000$。 **子任务 4 [30 分]** 没有额外的限制。