P14426 [JOISC 2014] 稻草人 / Scarecrows

在 JOI 村的一片广阔荒地上，竖立着 $N$ 个神社，村民们每年会绕着这些神社举行祭典。某日，村长听闻神社的神谕，决定在荒地上建造一个烟堆，且烟堆必须满足以下条件： - 烟堆必须是一个各边分别与东西方向或南北方向平行的长方形。 - 烟堆的西南角顶点和东北角顶点上必须各有一个神社。 - 烟堆的内部（不包括边界）不能有神社。 当然，神社是神圣的，不允许移动。请问，满足神谕要求的烟堆可能有多少个？ **问题** 给定神社的位置，编写一个程序，计算满足神谕条件的烟堆位置的个数。

从标准输入读取以下数据： - 第一行包含一个整数 $N$，表示有 $N$ 个神社。 - 接下来的 $N$ 行中，第 $i$ 行（$1 \le i \le N$）包含两个整数 $X_i$、$Y_i$，以空格分隔。JOI 村的荒地用 $xy$ 坐标平面表示，其中 $x$ 轴正方向为东，$y$ 轴正方向为北。第 $i$ 个神社位于坐标 $(X_i, Y_i)$。

在标准输出中，输出一行，表示满足神谕条件的烟堆位置的个数。

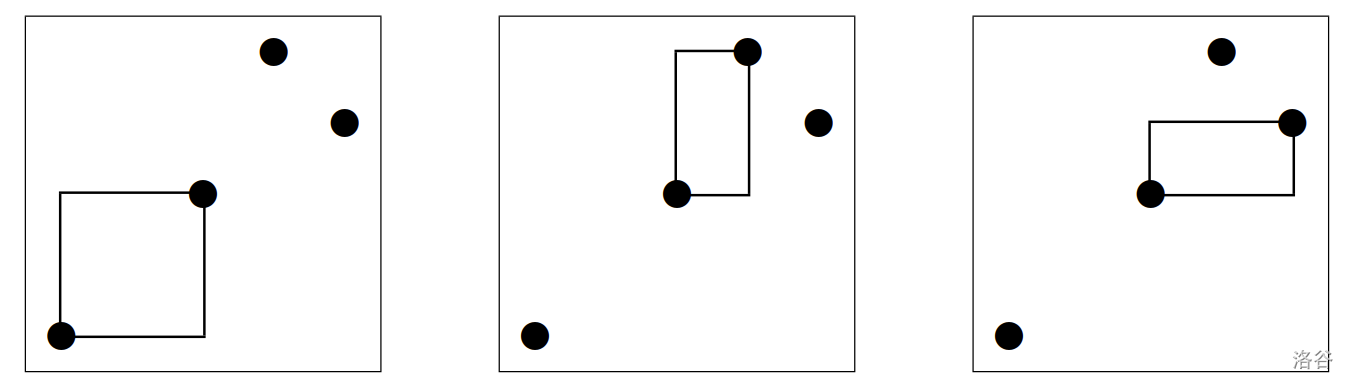
### 样例 1 解释 在该示例中，满足神谕条件的田地位置共有以下 3 个（如下图所示）： - 以点 $(0, 0)$ 为西南顶点、点 $(2, 2)$ 为东北顶点的长方形。 - 以点 $(2, 2)$ 为西南顶点、点 $(3, 4)$ 为东北顶点的长方形。 - 以点 $(2, 2)$ 为西南顶点、点 $(4, 3)$ 为东北顶点的长方形。 :::align{center}  ::: ### 样例 2 解释 :::align{center}  ::: ### 数据范围 所有输入数据均满足以下条件： - $1 \le N \le 200\,000$ - $0 \le X_i \le 1\,000\,000\,000$（$1 \le i \le N$） - $0 \le Y_i \le 1\,000\,000\,000$（$1 \le i \le N$） - $X_i$（$1 \le i \le N$）两两互不相同 - $Y_i$（$1 \le i \le N$）两两互不相同 ### 子任务 **子任务 1 [5 分]** - 满足 $N \le 400$ **子任务 2 [10 分]** - 满足 $N \le 5\,000$ **子任务 3 [85 分]** 无额外限制。 翻译由 Qwen3-235B 完成