P14428 [JOISC 2014] 二人的星座 / Constellation 2

JOI 酱和 IOI 酱是亲密无间的好友。某日，她们决定在山顶的观景台上进行天文观测。 在观景台上，可以观测到 $N$ 颗星星。每颗星星被赋予从 $1$ 到 $N$ 的编号，并且每颗星星呈现红色、蓝色或黄色中的一种颜色。 在观景台上观测到的星星被表示为坐标平面上的点。在该坐标平面中，第 $i$ 颗星星（$1 \le i \le N$）对应于点 $P_i(X_i, Y_i)$。坐标平面上的点 $P_1, \dots, P_N$ 两两互不相同，且任意三点不共线。 JOI 酱和 IOI 酱决定创造一个名为 **JOIOI 座** 的星座。她们首先考虑用红色、蓝色、黄色各一颗星星构成一个三角形，称这样的三角形为“**良好三角形**”。 两人决定将满足以下条件的两组良好三角形（不考虑顺序）作为 **JOIOI 座** 的候选： - 两个良好三角形（包括三角形的边界和内部）没有公共点。也就是说，两个良好三角形既不重叠，也没有一个包含另一个的情况。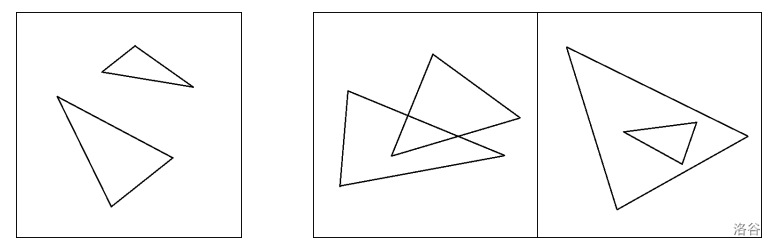 :::align{center}  左图：满足条件的样例 右图：不满足条件的样例 ::: JOI 酱和 IOI 酱决定统计可以作为 **JOIOI 座** 候选的方案总数。需要注意的是，即使构成 **JOIOI 座** 候选的 6 颗星星完全相同，只要构成“良好三角形”的连接方式不同，就将它们视为不同的候选方案进行计数。 **问题** 给定在观景台上观测到的星星信息，编写一个程序，输出 **JOIOI 座** 候选方案的总数。

从标准输入读取以下数据： - 第 1 行包含一个整数 $N$，表示在观景台上观测到的星星数量。 - 接下来的 $N$ 行中的第 $i$ 行（$1 \le i \le N$）包含三个整数 $X_i, Y_i, C_i$，以空格分隔。这表示第 $i$ 颗星星的坐标为 $P_i(X_i, Y_i)$，而 $C_i$ 表示第 $i$ 颗星星的颜色：若 $C_i = 0$，则为红色；若 $C_i = 1$，则为蓝色；若 $C_i = 2$，则为黄色。

在标准输出上，输出一个整数，表示 **JOIOI 座** 候选方案的总数，占一行。

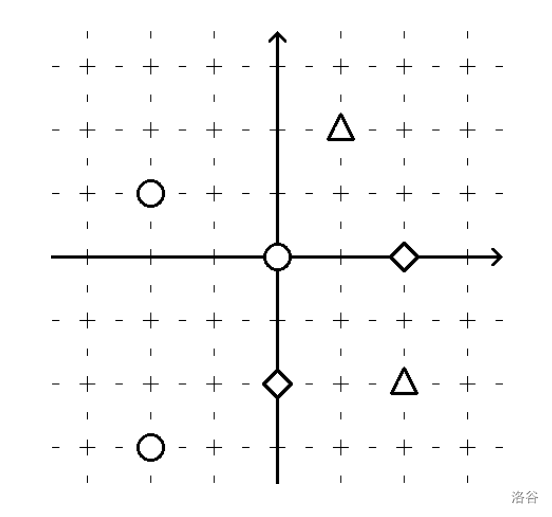
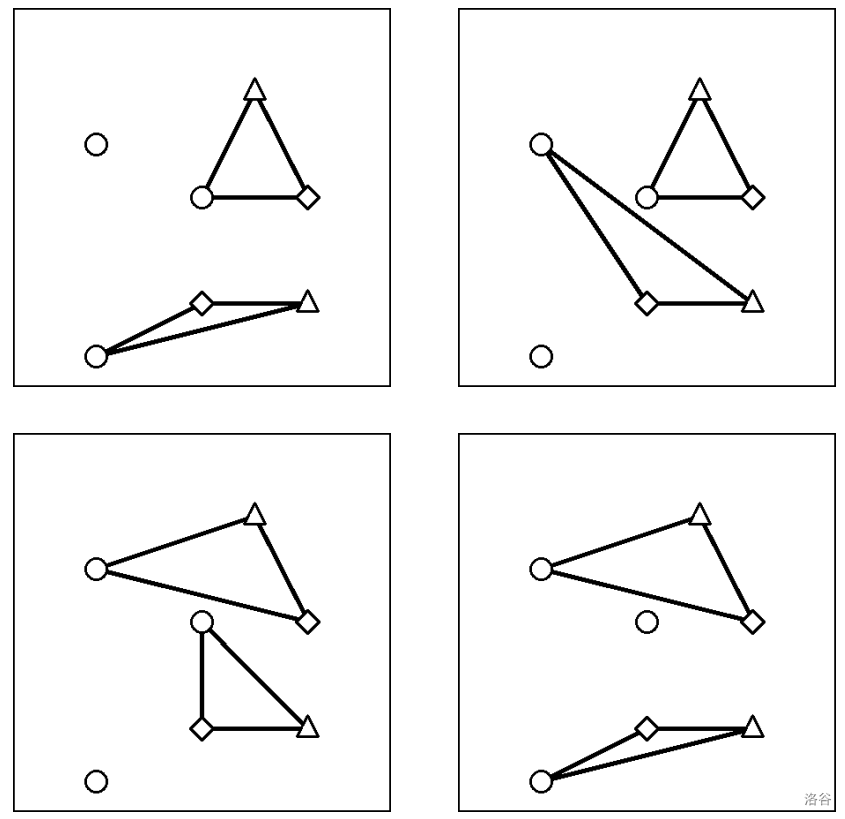
### 样例 1 解释 在该输入示例中，星星的分布如图所示。图中，红色星星用圆形表示，蓝色星星用菱形表示，黄色星星用三角形表示。 :::align{center}  ::: 在该输入示例中，**JOIOI 座** 的候选方案共有以下 4 种。 :::align{center}  ::: ### 数据范围 所有输入数据均满足以下条件： - $6 \le N \le 3\,000$ - $-100\,000 \le X_i \le 100\,000$ - $-100\,000 \le Y_i \le 100\,000$ - $0 \le C_i \le 2$ - 每种颜色的星星至少存在一颗 - $P_i \ne P_j$（对所有 $1 \le i < j \le N$） - $P_i, P_j, P_k$ 不共线（对所有 $1 \le i < j < k \le N$） ### 子任务 **子任务 1 [15 分]** - 满足 $N \le 30$。 **子任务 2 [40 分]** - 满足 $N \le 300$。 **子任务 3 [45 分]** 无额外限制。 翻译由 Qwen3-235B 完成