P1442 Falling Iron Ball

In a 2D coordinate system, there are $n$ platforms (a platform is defined as a horizontal open line segment whose two endpoints share the same $y$-coordinate; an open line segment means its two endpoints are not part of the segment itself) and one iron ball. If there is no object directly below, the ball falls $1$ unit length per second. Each time the ball lands on a platform, the player may choose to roll horizontally to the left or to the right. The rolling speed is $1$ unit length per second. Because the iron ball is fragile, the height of each single drop must not exceed $h$. Design a strategy to make the ball reach the ground as quickly as possible without breaking. 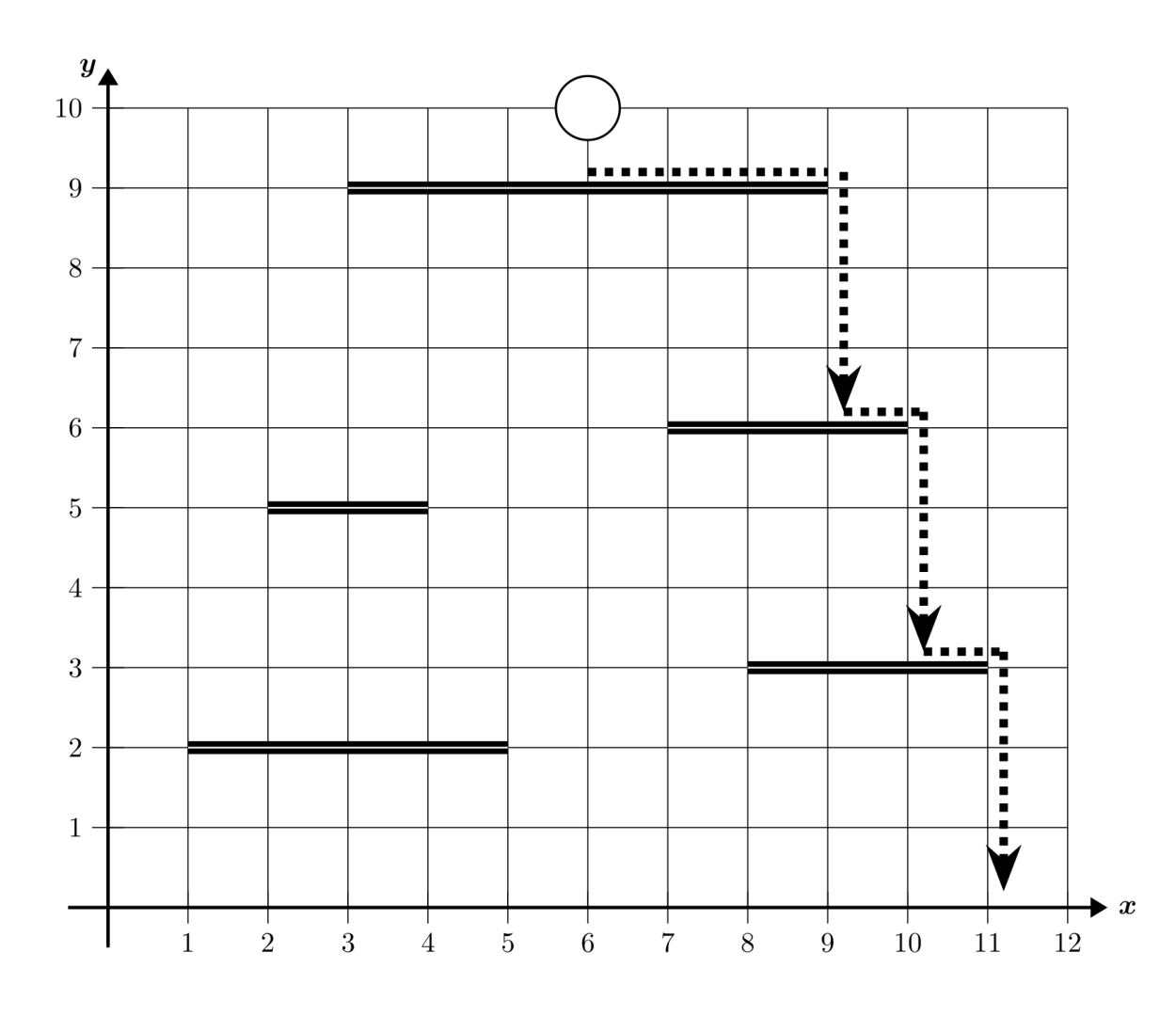Assume the ground has height $0$ and is infinitely wide. The ball’s size is negligible compared to the platforms and can be treated as a point mass. Please note: the ball begins to fall as soon as it reaches an endpoint of a platform; it does not need to roll into the next cell. For example, in the figure below, the ball at $(9, 9)$ has already started to fall. 

The first line contains two integers representing the number of platforms $n$ and the maximum allowed drop height $h$. The second line contains two integers $x, y$, indicating that the iron ball starts at position $(x, y)$. Lines $3$ to $n + 2$: each line contains three integers. On line $i + 2$, the integers $h_i, l_i, r_i$ denote the $y$-coordinate $h_i$ of the $i$-th platform and the $x$-coordinates $l_i, r_i$ of its left and right endpoints, respectively.

Output one line with a single integer: the minimum total time to reach the ground.

Constraints and Conventions For all test points, it is guaranteed that: - $1 \leq n \leq 10^5$. - $1 \leq x, y, h, h_i, l_i, r_i \leq 10^9$, $l_i \leq r_i$. - All $h_i$ are pairwise distinct; all $l_i$ and $r_i$ are also pairwise distinct; and for any $i \neq j$, it holds that $l_i \neq r_j$. - The testdata guarantees there is a solution, and the final answer does not exceed $10^9$. Translated by ChatGPT 5