P14431 [JOISC 2013] 有趣的图像收集 / Collecting Images is Fun

JOI 君非常喜欢收集大量图片，并拥有许多图像。最近，JOI 君发现自己因收集过多图片而导致硬盘容量略显不足。他没有购买新硬盘的预算，但删除已有的图片对他而言是极大的痛苦，因此他决定通过巧妙地压缩图片来减少存储空间。 每张图片由 $2^N$ 行 $2^N$ 列的正方形像素网格表示，共计 $2^N \times 2^N$ 个像素。每个像素为白色或黑色。 JOI 君采用以下方法对这类图像进行压缩： - 若图像内所有像素颜色相同，则仅记录该颜色。此时压缩后数据的大小为 $1$。 - 否则，将图像分割为四个较小的子图像。若原图像为 $2^k$ 行 $2^k$ 列，则沿纵向和横向的中心线进行分割，得到四个 $2^{k-1}$ 行 $2^{k-1}$ 列的子图像。对这些较小的子图像递归应用相同的压缩方法。此时，压缩后数据的大小为四个子图像压缩后数据大小之和再加 $1$。 JOI 君对这种方法是否能有效压缩图像感到不安，因此决定对多种图像进行实验。实验方法如下： - 首先准备一张所有像素均为白色的图像。 - 对于 $i = 1, \cdots, Q$，执行以下操作：若 $T_i = 0$，则反转从上数第 $X_i$ 行的 $2^N$ 个像素的颜色；若 $T_i = 1$，则反转从左数第 $X_i$ 列的 $2^N$ 个像素的颜色。即，记从上第 $a$ 行、从左第 $b$ 列的像素为 $(a,b)$，对于每个 $i$，当 $T_i = 0$ 时，对满足 $1 \leq b \leq 2^N$ 的像素 $(X_i,b)$ 执行颜色反转（白变黑，黑变白）；当 $T_i = 1$ 时，对满足 $1 \leq a \leq 2^N$ 的像素 $(a,X_i)$ 执行颜色反转。 - 对于每个 $i$，在第 $i$ 次操作结束后，调查按 JOI 君方法压缩该图像后所得数据的大小。 为了在实验中执行尽可能多的操作，需要高效计算压缩后数据的大小。 ### 任务 给定表示图像大小的整数 $N$、操作次数 $Q$ 以及 $Q$ 次操作的描述，编写程序计算每次操作结束后，按 JOI 君方法压缩图像所得数据的大小。

从标准输入读取以下输入数据： - 第 $1$ 行包含两个以空格分隔的整数 $N, Q$，表示图像大小为 $2^N$ 行 $2^N$ 列，且将执行 $Q$ 次操作。 - 接下来的 $Q$ 行描述操作指令。第 $i$ 行（$1 \leq i \leq Q$）包含两个以空格分隔的整数 $T_i, X_i$（$0 \leq T_i \leq 1$ 且 $1 \leq X_i \leq 2^N$），表示第 $i$ 次操作：若 $T_i = 0$ 则反转从上数第 $X_i$ 行的所有像素颜色；若 $T_i = 1$ 则反转从左数第 $X_i$ 列的所有像素颜色。

向标准输出输出 $Q$ 行。第 $i$ 行（$1 \leq i \leq Q$）应包含一个整数，表示第 $i$ 次操作结束后，按 JOI 君方法压缩图像所得数据的大小。

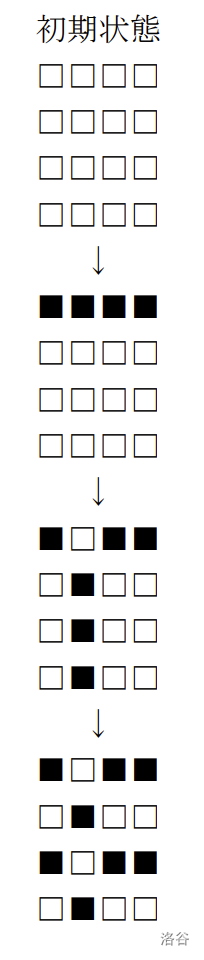
### 样例 1 解释 在这个例子中，$Q=3$ 次操作按以下方式进行： :::align{center}  ::: ### 限制 所有输入数据满足以下条件： - $1 \leq N \leq 20$ - $1 \leq Q \leq 2\,000\,000$ ### 子任务 #### 子任务 1 [10 分] 满足以下条件： - $N \leq 6$ - $Q \leq 128$ #### 子任务 2 [20 分] 满足以下条件： - $N \leq 10$ - $Q \leq 2\,048$ #### 子任务 3 [70 分] 无额外限制。 翻译由 DeepSeek V3 完成