P14432 [JOISC 2013] 通信阻塞 / Communication Jamming

JOI 国位于平面上。国内有 $N$ 个村庄，村庄编号为 $1$ 到 $N$。村庄 $i$ 被视为位于坐标 $(i,0)$ 的点。目前，JOI 国计划建设连接村庄的通信线路。为应对故障，计划建设两套系统，分别称为 **系统 1** 和 **系统 2**。 系统 $k$ 包含 $M_k$ 个枢纽和 $N + M_k - 1$ 条线路。系统 $k$ 的枢纽编号为 $1$ 到 $M_k$，枢纽 $j$ 被视为位于坐标 $(X_{kj}, Y_{kj})$ 的点。系统 $k$ 的每条线路连接村庄与系统 $k$ 的枢纽，或连接系统 $k$ 的枢纽之间。每条线路被视为连接两端的线段。保证任意两条线路除端点外没有其他公共点。系统 $1$ 的枢纽 $j$ 的 $y$ 坐标 $Y_{1j}$ 大于 $0$；系统 $2$ 的枢纽 $j$ 的 $y$ 坐标 $Y_{2j}$ 小于 $0$。 若两个地点能通过线路间接连接，则称它们可以通信。即，若能通过沿线路反复移动从一个地点到达另一个地点，则这两个地点可以通信。仅考虑系统 $1$ 的线路或仅考虑系统 $2$ 的线路时，任意两个村庄及枢纽均可以通信。 下图是通信线路的示例。灰色圆点表示系统 $1$ 的枢纽，黑色圆点表示系统 $2$ 的枢纽，白色圆点表示村庄。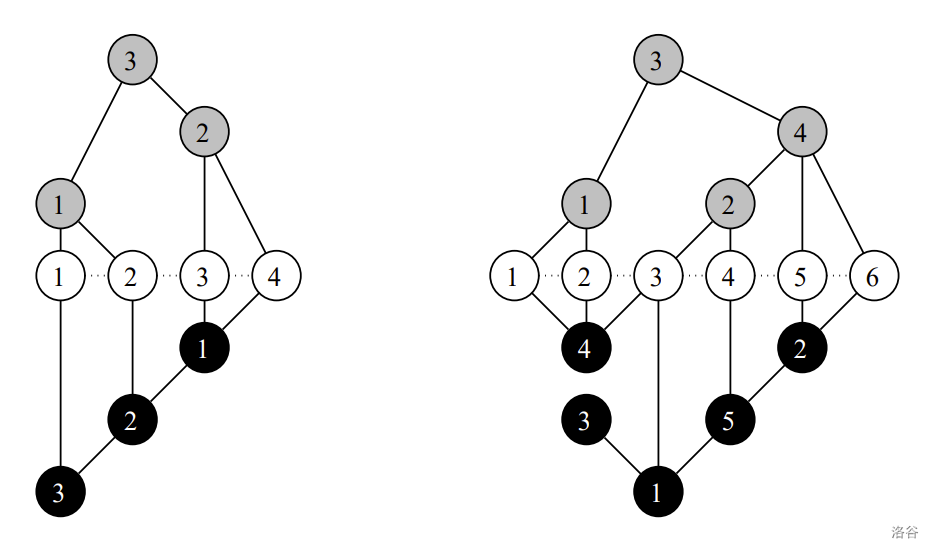 :::align{center}  左图对应样例 1，右图对应样例 2 ::: 在计划讨论中，需研究在外部攻击下通信的可持续性。外部攻击由两个数 $A$, $B$（$A \geq 0$, $B \leq 0$）描述，假设其会破坏所有 $y$ 坐标大于 $A$ 的枢纽和所有 $y$ 坐标小于 $B$ 的枢纽。枢纽被破坏后，经其转发的通信将无法进行。 ### 任务 给定村庄及各系统的信息，同时给出 $Q$ 个查询。每个查询 $q$ 由一个整数 $A_q$ 表示，意味着所有 $y$ 坐标大于 $A_q$ 的枢纽将被破坏。对于每个查询，求一个整数 $B_q$（$B_q \leq 0$），使得即使破坏所有 $y$ 坐标大于 $A_q$ 的枢纽和所有 $y$ 坐标小于 $B_q$ 的枢纽，所有村庄之间仍能保持通信，且 $B_q$ 是满足条件的最大值。

从标准输入读取以下输入数据： - 第 $1$ 行包含四个以空格分隔的整数 $N, M_1, M_2, Q$。 - 接下来的 $M_1 + (N + M_1 - 1)$ 行描述系统 $1$ 的信息： - 前 $M_1$ 行中，第 $i$ 行（$1 \leq i \leq M_1$）包含两个整数 $X_{1i}, Y_{1i}$。 - 后续 $N + M_1 - 1$ 行中，第 $i$ 行（$1 \leq i \leq N + M_1 - 1$）包含三个整数 $T_{1i}, C_{1i}, D_{1i}$（$T_{1i} = 1, 2$）： - 若 $T_{1i} = 1$，则线路 $i$ 连接村庄 $C_{1i}$ 与枢纽 $D_{1i}$（$1 \leq C_{1i} \leq N$，$1 \leq D_{1i} \leq M_1$）。 - 若 $T_{1i} = 2$，则线路 $i$ 连接枢纽 $C_{1i}$ 与枢纽 $D_{1i}$（$1 \leq C_{1i}, D_{1i} \leq M_1$，且 $C_{1i} \neq D_{1i}$）。 - 接下来的 $M_2 + (N + M_2 - 1)$ 行描述系统 $2$ 的信息： - 前 $M_2$ 行中，第 $i$ 行（$1 \leq i \leq M_2$）包含两个整数 $X_{2i}, Y_{2i}$。 - 后续 $N + M_2 - 1$ 行中，第 $i$ 行（$1 \leq i \leq N + M_2 - 1$）包含三个整数 $T_{2i}, C_{2i}, D_{2i}$（$T_{2i} = 1, 2$）： - 若 $T_{2i} = 1$，则线路 $i$ 连接村庄 $C_{2i}$ 与枢纽 $D_{2i}$（$1 \leq C_{2i} \leq N$，$1 \leq D_{2i} \leq M_2$）。 - 若 $T_{2i} = 2$，则线路 $i$ 连接枢纽 $C_{2i}$ 与枢纽 $D_{2i}$（$1 \leq C_{2i}, D_{2i} \leq M_2$，且 $C_{2i} \neq D_{2i}$）。 - 接下来的 $Q$ 行中，第 $i$ 行（$1 \leq i \leq Q$）包含一个整数 $A_i$。

向标准输出输出 $Q$ 行。第 $i$ 行（$1 \leq i \leq Q$）输出一个整数 $B_i$，表示对查询 $i$ 的答案。若答案为 $0$，不得输出 $-0$。

### 限制 所有输入数据满足以下条件： - $1 \leq N, M_1, M_2 \leq 100\,000$ - $-1\,000\,000\,000 \leq X_{1i} \leq 1\,000\,000\,000$ ($1 \leq i \leq M_1$) - $-1\,000\,000\,000 \leq X_{2i} \leq 1\,000\,000\,000$ ($1 \leq i \leq M_2$) - $1 \leq Y_{1i} \leq 1\,000\,000\,000$ ($1 \leq i \leq M_1$) - $-1\,000\,000\,000 \leq Y_{2i} \leq -1$ ($1 \leq i \leq M_2$) - $X_{1i} \neq X_{1j}$ 或 $Y_{1i} \neq Y_{1j}$ ($1 \leq i,j \leq M_1$ 且 $i \neq j$) - $X_{2i} \neq X_{2j}$ 或 $Y_{2i} \neq Y_{2j}$ ($1 \leq i,j \leq M_2$ 且 $i \neq j$) - $1 \leq Q \leq 100\,000$ - $0 \leq A_i \leq 1\,000\,000\,000$ ($1 \leq i \leq Q$) - 任意两条线路除端点外没有其他公共点 - 仅考虑系统 $1$ 的线路或仅考虑系统 $2$ 的线路时，任意两个村庄及枢纽均可以通信 ### 子任务 #### 子任务 1 [20 分] 满足以下条件： - $N, M_1, M_2 \leq 1\,000$ - $Q \leq 1\,000$ #### 子任务 2 [80 分] 无额外限制。 翻译由 DeepSeek V3 完成