P14438 [JOISC 2013] 切割蛋糕 / Cake

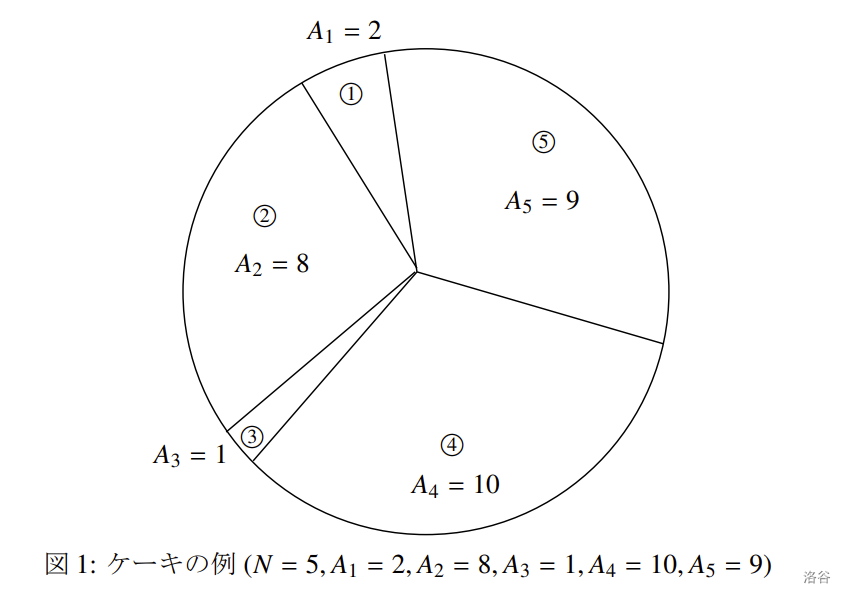
JOI 君和 IOI 酱是双胞胎兄妹。JOI 君最近迷上了烘焙，今天他刚烤好一个蛋糕准备享用，但烤好的香味引来了 IOI 酱，于是两人决定平分这个蛋糕。 蛋糕是圆形的。从某一点沿放射状切入，将蛋糕切分成 $N$ 块，并按逆时针方向为这些块编号 $1$ 到 $N$。也就是说，对于 $1 \leq i \leq N$，第 $i$ 块与第 $i-1$ 块和第 $i+1$ 块相邻（其中视第 $0$ 块为第 $N$ 块，第 $N+1$ 块为第 $1$ 块）。第 $i$ 块的大小为 $A_i$，但由于切工十分拙劣，所有 $A_i$ 的值均互不相同。 :::align{center}  ::: 决定将这 $N$ 块蛋糕分给 JOI 君和 IOI 酱。分配方式如下： - 首先由 JOI 君从 $N$ 块中选择 $1$ 块取走。 - 随后从 IOI 酱开始，IOI 酱和 JOI 君轮流从剩余蛋糕块中每次取 1 块。但（由于两人不擅长取蛋糕且要避免破坏蛋糕形状）只能取那些至少有一侧相邻蛋糕块已被取走的蛋糕块。当有多块可取的蛋糕块时，选择其中 **最大** 的一块取走。 JOI 君想知道，对于每一块蛋糕，若他最初选择取走该块，则最终自己获得的所有蛋糕块大小之和是多少。 ### 任务 给定蛋糕块的数量 $N$ 以及 $N$ 块蛋糕的大小信息，编写程序计算对于每一块蛋糕，若最初取走该块，则 JOI 君最终获得的蛋糕块大小之和。

从标准输入读取以下输入数据： - 第 $1$ 行包含一个整数 $N$，表示蛋糕被切分为 $N$ 块。 - 后续 $N$ 行中，第 $i$ 行（$1 \leq i \leq N$）包含一个整数 $A_i$，表示第 $i$ 块蛋糕的大小。

向标准输出输出 $N$ 行。第 $i$ 行（$1 \leq i \leq N$）输出一个整数，表示若最初取走第 $i$ 块蛋糕，则 JOI 君最终获得的蛋糕块大小之和。

### 样例 1 解释 此示例对应题目中图示的情况。 例如，假设最初取走第 $1$ 块。此时： - 剩余蛋糕块中「至少有一侧相邻蛋糕块已被取走」的是第 $2$ 块和第 $5$ 块，由于第 $5$ 块较大，因此接下来取走第 $5$ 块。 - 类似地，接下来比较第 $2$ 块和第 $4$ 块，由于第 $4$ 块较大，因此取走第 $4$ 块。 - 接着比较第 $2$ 块和第 $3$ 块，由于第 $2$ 块较大，因此取走第 $2$ 块。 - 最后仅剩第 $3$ 块，因此取走第 $3$ 块。 即蛋糕块的取走顺序为： 第 $1$ 块 ($2$) → 第 $5$ 块 ($9$) → 第 $4$ 块 ($10$) → 第 $2$ 块 ($8$) → 第 $3$ 块 ($1$) （括号内为蛋糕块大小） 因此 JOI 君取走的蛋糕块为第 $1$、$4$、$3$ 块，其大小之和为 $13$，故在第 $1$ 行输出 $13$。最初取走第 $1$ 块以外的其他块时，也以类似方式计算。 ### 限制 所有输入数据满足以下条件： - $2 \leq N \leq 300\,000$ - $1 \leq A_i \leq 1\,000\,000\,000$ ($1 \leq i \leq N$) ### 子任务 #### 子任务 1 [10 分] - 满足 $N \leq 5000$ #### 子任务 2 [90 分] 无额外限制 翻译由 DeepSeek V3 完成