P14450 [ICPC 2025 Xi'an R] Directed Acyclic Graph

Given two integers $n$ and $m$, you need to construct a directed acyclic graph (DAG) $G = (V, E)$ with exactly $n$ vertices and $m$ edges. In the graph $G$, a vertex $v$ is called $\textit{reachable}$ from vertex $u$ if and only if there exists a path in the graph that starts at vertex $u$ and ends at vertex $v$. For a non-empty set of vertices $A\subseteq V$, a vertex $w$ is defined as $\textit{good}$ for $A$ if and only if it is reachable from $\textbf{every}$ vertex in $A$, and we denote $f(A)$ as the set of all good vertices for $A$. The graph you constructed should satisfy both of the following constraints: - For every vertex $i$ ($1\le i\le n$), it is reachable from vertex $1$. - There exist $k$ distinct non-empty sets of vertices $S_1, S_2, \ldots, S_k$, such that $f(S_1), f(S_2), \ldots, f(S_k)$ are pairwise distinct. Note that $f(S_i)$ can be empty. To prove the graph $G$ you constructed satisfies the second constraint, you also need to provide $k$ sets $S_1, S_2,\ldots, S_k$ that satisfy the second constraint.

The only line of the input contains three integers $n, m$, and $k$. There are only $2$ tests in this problem: - $n = 5$, $m = 6$, $k = 6$; - $n = 100$, $m = 128$, $k = 16\,000$.

The first $m$ lines of the output describe the graph $G$ you construct. Each line contains two integers $u, v$ representing an edge from $u$ to $v$ in the graph. The next $k$ lines of the output describe the $k$ sets of vertices you provide. The $i$-th line first contains the size of the set $S_i$, followed by the $|S_i|$ numbers representing each vertex in the set.

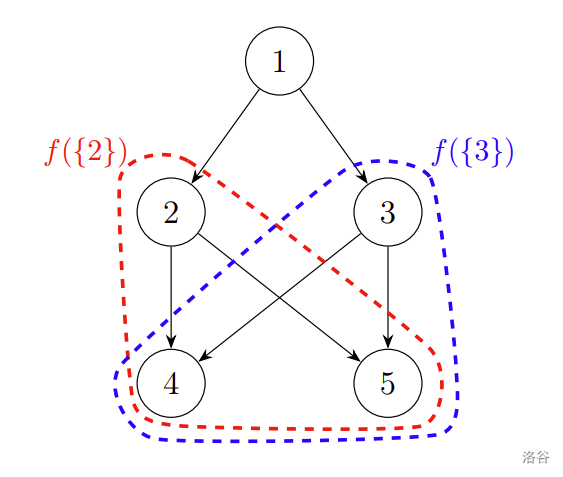
In the example, the output constructs a graph with $n = 5$ vertices and $m = 6$ edges. The corresponding $k = 6$ sets are $S_1 = \{1\}, S_2 = \{2\}, S_3 = \{3\}, S_4 = \{4\}, S_5 = \{5\}, S_6 = \{2, 3\}$. Here, vertices $4$ and $5$ can both be reached from any element in $S_6 = \{2, 3\}$, so $f(\{2, 3\}) = \{4, 5\}$. Together with $f(S_1) = \{1, 2, 3, 4, 5\}, f(S_2) = \{2, 4, 5\}, f(S_3) = \{3, 4, 5\}, f(S_4) = \{4\}, f(S_5) = \{5\}$, these sets are all distinct, satisfying the constraints. :::align{center}  :::