P14452 [ICPC 2025 Xi'an R] Follow the Penguins

有 $n$ 只企鹅站在数轴上。第 $i$ 只企鹅最初位于坐标 $a_i$ 处。保证所有的 $a_i$ 互不相同。 每只企鹅都会选择一个目标企鹅，记为 $t_i$（$1 \leq t_i \leq n$，且 $t_i \neq i$）。在时间 $0$ 时，所有企鹅同时开始移动。每只企鹅以每秒 $0.5$ 个单位长度的速度，朝着其目标企鹅当前所在的位置移动。 当第 $i$ 只企鹅与它的目标企鹅 $t_i$ 相遇时（即二者在同一时刻到达同一坐标），它会立即停止移动。对于每只企鹅，请你求出它停止移动的时间。 可以证明，每只企鹅都会在有限的时间内停止，且停止时间总是一个整数。

输入的第一行包含一个整数 $n$（$2 \leq n \leq 5 \cdot 10^5$），表示企鹅的数量。 第二行包含 $n$ 个整数 $t_1, t_2, \ldots, t_n$（$1 \leq t_i \leq n$，且 $t_i \neq i$），其中 $t_i$ 表示第 $i$ 只企鹅选择的目标企鹅编号。 第三行包含 $n$ 个互不相同的整数 $a_1, a_2, \ldots, a_n$（$-5 \cdot 10^8 \leq a_i \leq 5 \cdot 10^8$），其中 $a_i$ 表示第 $i$ 只企鹅的初始坐标。

输出一行，包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 只企鹅停止移动的时间（单位为秒）。

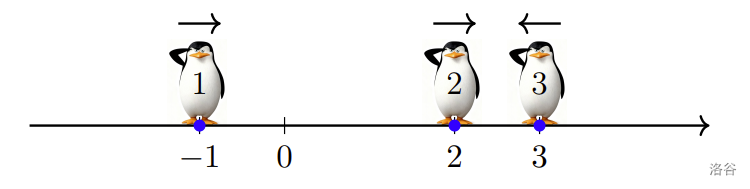
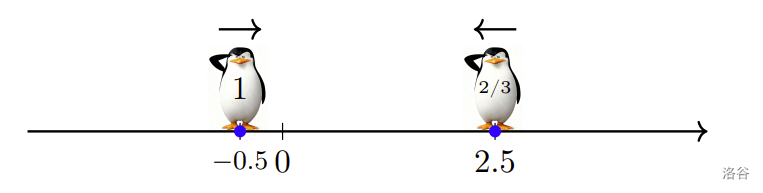
在第一个样例中： 最初，第 2 只企鹅位于第 1 只企鹅的右侧，因此第 1 只企鹅向右移动。同样地，第 2 只企鹅也向右移动，而第 3 只企鹅向左移动。它们在数轴上的初始位置如下图所示： :::align{center}  ::: 在第 $1$ 秒时，第 2 只企鹅与第 3 只企鹅在 $x = 2.5$ 处相遇，此时第 2 只企鹅停止移动。 :::align{center}  ::: 此时，第 1 只企鹅的位置是 $x = -0.5$，第 2 只企鹅的位置是 $x = 2.5$，二者之间的距离为 $3$。由于第 1 只企鹅以每秒 $0.5$ 个单位的速度移动，它还需要 $6$ 秒才能到达第 2 只企鹅。因此，第 1 只企鹅在第 $7$ 秒时停止。 在第 1 只企鹅停止之前，第 3 只企鹅会在第 $4$ 秒与它相遇。因此，答案分别为 $7$、$1$ 和 $4$。 翻译由 ChatGPT-5 完成