P14452 [ICPC 2025 Xi'an R] Follow the Penguins

There are $n$ penguins standing on a number line. The $i$-th penguin is initially located at coordinate $a_i$. It is guaranteed that all $a_i$-s are pairwise distinct. Each penguin chooses a target penguin, denoted by $t_i$ ($1 \leq t_i \leq n$, $t_i \neq i$). At time $0$, all penguins start moving simultaneously. Each one runs towards the current position of its target penguin at a constant speed of $0.5$ units per second. When penguin $i$ meets penguin $t_i$, it stops immediately. For every penguin, determine the time when it stops moving. Here, penguin $i$ meets penguin $t_i$ if and only if they are at the same coordinate at the same time. It can be proven that every penguin will stop moving within a finite amount of time, and the stopping time is always an integer.

The first line of the input contains a single integer $n$ ($2 \leq n \leq 5 \cdot 10^5$), which is the number of penguins. The second line of the input contains $n$ integers $t_1, t_2, \ldots, t_n$ ($1 \leq t_i \leq n$, $t_i \neq i$), where $t_i$ is the target chosen by the $i$-th penguin. The third line of the input contains $n$ distinct integers $a_1, a_2, \ldots, a_n$ ($-5\cdot 10^8\leq a_i\leq 5 \cdot 10^8$), where $a_i$ is the initial coordinate of the $i$-th penguin.

Output a single line containing $n$ integers, where the $i$-th integer represents the time (in seconds) when the $i$-th penguin stops moving.

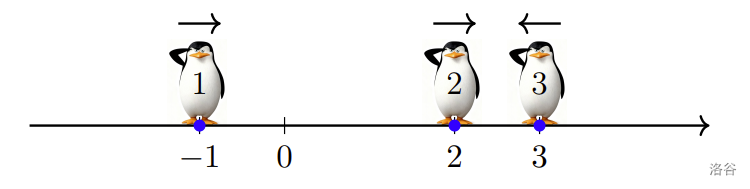
In the example, initially, since the second penguin is in the positive direction of the first penguin, the first penguin runs in the positive direction. Similarly, the second penguin runs in the positive direction, while the third penguin runs in the negative direction. The initial positions of the three penguins on the number line are shown in the figure below: :::align{center}  ::: At second $1$, the second penguin and the third penguin meet at $x = 2.5$, at which point the second penguin stops moving. 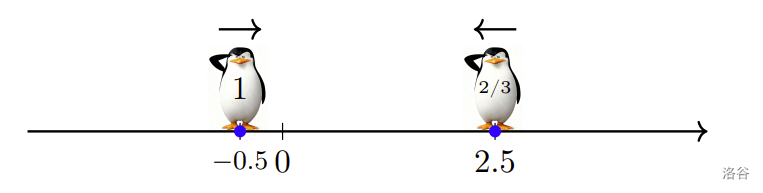:::align{center}  ::: At this moment, the first penguin is at $-0.5$, and the second penguin is at $2.5$. The distance between them is $3$. Since the first penguin runs at a speed of $0.5$ units per second, it will take $6$ more seconds to reach the second penguin. Therefore, the first penguin stops moving at second $7$. Before the first penguin stops, the third penguin meets it at second $4$. So the answers are $7$, $1$, and $4$, respectively.