P14455 [ICPC 2025 Xi'an R] Imagined Holly

给定一个非负整数矩阵 $A$，大小为 $n \times n$。对于一棵有 $n$ 个顶点的树（顶点编号为 $1$ 到 $n$），当且仅当它满足以下条件时，我们称这棵树为 **冬青树**： - 对于任意两个顶点 $u$ 和 $v$（$1 \leq u, v \leq n$），矩阵中的 $A_{u,v}$ 等于从 $u$ 到 $v$ 的简单路径上所有顶点编号的按位异或和。 你的任务是构造一棵冬青树。保证至少存在一棵满足条件的冬青树。

输入的第一行包含一个整数 $n$（$2 \leq n \leq 2000$），表示矩阵 $A$ 的大小。 接下来 $n$ 行描述矩阵 $A$。第 $i$ 行包含 $n - i + 1$ 个整数，分别是 $A_{i,i}, A_{i, i+1}, \ldots, A_{i, n}$（$0 \leq A_{i, j} < 2^{11}$）。 注意，对于所有 $1 \leq i, j \leq n$，都有 $A_{i, j} = A_{j, i}$。 保证至少存在一棵冬青树。

输出 $n - 1$ 行，每行输出两个整数 $u$ 和 $v$（$1 \leq u, v \leq n$），表示冬青树中的一条边。

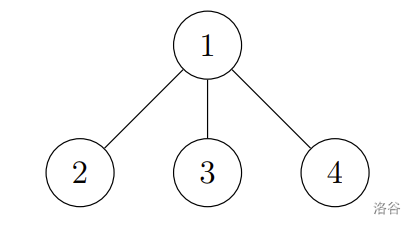
在第二个示例中，输出中的树如下图所示： :::align{center}  ::: 该树是一棵冬青树。例如，对于顶点对 $(2, 4)$，从 $2$ 到 $4$ 的简单路径经过顶点 $2 \rightarrow 1 \rightarrow 4$，这些编号按位异或为： $$2 \oplus 1 \oplus 4 = 7,$$ 这与输入中给出的 $A_{2,4} = 7$ 一致。 ——翻译由 ChatGPT-5 完成