P14455 [ICPC 2025 Xi'an R] Imagined Holly

Given a non-negative integer matrix $A$ of size $n \times n$. For a tree with $n$ vertices, numbered from $1$ to $n$, we call it a $\textit{holly tree}$ if and only if: - For any pair of vertices $u$ and $v$ ($1 \leq u, v \leq n$), $A_{u, v}$ equals the bitwise XOR sum of the indices of the vertices on the simple path from $u$ to $v$ in the tree. Your task is to construct a holly tree. It is guaranteed that such a holly tree always exists.

The first line of the input contains an integer $n$ ($2 \leq n \leq 2000$), which is the size of matrix $A$. The next $n$ lines of the input describe the matrix $A$. The $i$-th line contains $n - i + 1$ integers $A_{i, i}, A_{i, i + 1}, \ldots, A_{i, n}$ ($0 \leq A_{i, j} < 2^{11}$). Note that $A_{i, j} = A_{j, i}$ holds for all $1 \leq i, j \leq n$. It is guaranteed that such a holly tree always exists.

Output $n - 1$ lines, each containing two integers $u$ and $v$ ($1 \leq u, v \leq n$), representing an edge of the holly tree.

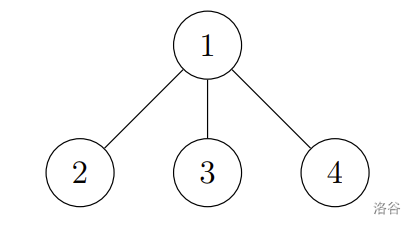
In the second example, the tree in the output is shown in the following figure: :::align{center}  ::: This tree is a holly tree. For example, for the pair of vertices $(2, 4)$, the simple path from $1$ to $4$ includes vertices $2, 1$, and $4$, with a bitwise XOR sum of $2 \oplus 1 \oplus 4 = 7$, which satisfies the constraint $A_{2, 4} = 7$ given in the input.