P14486 [集训队互测 2018] 北校门外的未来
题目背景
> 如果你不想阅读故事,请直接跳到题意部分。
转眼间,已是三年流转。
夏日法桐的绿荫,代替了秋季的萧索,衬托着 LCR 和神犇成长的背影。
身后的北校门,也不再是当年学生试图摧毁的,束缚自由的枷锁,而成了青春记忆的符号。
又到了神犇和 LCR 相遇的地方 —— 北校门外的树下。这棵神奇的树早已不是 K 项树的形态。每时每刻,它都以新的独特方式演绎着生命。
谁也没有开口,他和她静静地注视着魔法般生长的自然种子。初始时,这棵树只有一个点,LCR 将其标号为 $1$。此后,每过一段时间,就会有一个新节点从原有的某个点出生长出来,LCR 会给它分配一个尚未使用过的不超过 $n$ 的正整数编号。
树中生活着一些小精灵。它们总停留在节点上,如果一个精灵在编号 $u$ 的节点,那么它可以一步跳到任何编号 $v$ 的满足 $u,v$ 之间的简单路径上不存在异于 $u,v$ 的编号大于 $\min(u,v)$ 的点处。
在观察这棵树的过程中,LCR 产生了一些疑问。她想知道,对于一对节点编号 $u,v$,从节点 $u$ 跳到节点 $v$ 最少需要几步。
神犇轻松地解决了这些问题。最终,树渐渐停止了生长,但神犇仍然陶醉其中。
一只飘渺的手搭上了神犇的肩膀。他回过头,看到 LCR 正在微笑。
*“亲爱的少年,神犇君。”*
*“你是否想过,为什么精灵会依照我编号的法则而运动呢?”*
神犇一时语塞。瞬间,LCR 的手变得虚幻了起来,如同明灭的火炬。
*“你的成长,是这变化世界的一个切面。感谢你与我度过的时光。不要留恋 …… 我的随风飘散,正是与你们同在。”*
*“再见了,神犇君。”*
LCR 消失了,神犇机械地转过身,却发现背后的树也已消失无踪。
*“神犇,神犇 ……”* 茫然若失的神犇背后传来了渐行渐近的呼叫。神犇转过身,发现机房里的蒟蒻 LCA 正向他跑来。
*“又是一年毕业季了呢。学长你还好吗?”*
*“也许吧。”* 神犇望向校门外的树原先的位置,*“LCR 走了,但她的背影会吸引着我们的人生。”*
LCA 沉默了。他和神犇一同望向树消失的地方,持续片刻。
*“所谓中二的幻想,才是我们相对的有限的主观能动性唯一的立场吧,不要给自己设限啊,LCA。我们去追寻她 …… 追寻自然的精灵。也许这就是我们的初心也说不定。”*
这次是 LCA 目送神犇的背影渐行渐远了。
*“再见了,学长。”*
某少女附中,又迎来了新的一年。
那么,你能够回答 LCR 提出的问题吗?
题目描述
对于一棵树 $T=(V,E)$,$V$ 中每个点有一个互不相同的正整数标号。我们用点 $i$ 表示编号为 $i$ 的点。
定义这棵树的**谷图**为 $G(T)=(V,E')$。$G(T)$ 是无向简单图。存在边 $(u,v)\in E'$ 当且仅当在 $T$ 中,不存在一个异于 $u,v$ 的点 $x$ 满足 $x$ 在从 $u$ 到 $v$ 的简单路径上且其编号大于 $\min(u,v)$。
有一棵树 $T$,初始时只有一个点,编号为 $1$,接下来有 $q$ 次操作,操作有以下两种:
* $\texttt{1 u v}$ 表示加入一个编号为 $v$ 的节点并与当前编号为 $u$ 的节点相连(保证任何时刻不会有两个编号相同的节点);
* $\texttt{2 u v}$ 表示查询 $G(T)$ 中点 $u$ 到 $v$ 的最短路(每条边长度均为 $1$)。
请你回答所有查询。
输入格式
第一行两个整数 $n, q$,表示编号的最大可能值及询问个数。
接下来 $q$ 行每行三个整数 $\texttt{op u v}$,以题目描述中的格式描述一次操作。
输出格式
依次对于每一个 $\texttt{2}$ 类型的操作,输出一行一个整数表示其对应的答案。
说明/提示
### 样例 1 解释
最终的树 $T$ 和 $G(T)$ 如下:
:::align{center}
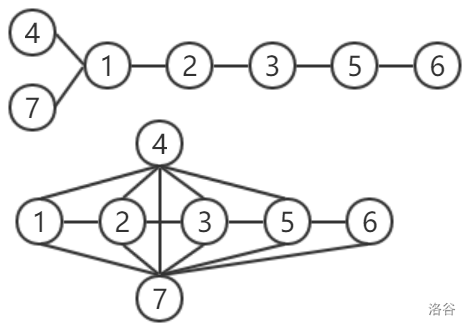
:::
第一次询问的路径:$1 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 6$;
第二次询问的路径:$1 \rightarrow 4 \rightarrow 5 \rightarrow 6$;
第三次询问的路径:$1 \rightarrow 7 \rightarrow 6$;
第四次询问的路径:$3 \rightarrow 5 \rightarrow 6$。
### 数据范围与提示
对于所有数据,$1\le n\le 10^5,1\le q\le 5\times 10^5$。
每个子任务详细的数据限制及约定如下(留空表示和上述所有数据的约定相同):
|子任务编号|分数|$n$|$q$|性质|
|:-:|:-:|:-:|:-:|:-:|
|$1$|$6$|$\le 100$|$\le 200$|无|
|$2$|$10$|$\le 5000$|$\le 10000$|^|
|$3$|$12$|$\le 5000$| ^ |^|
|$4$|$15$| ^ | ^ |一、二|
|$5$|$12$| ^ | ^ |二|
|$6$|$10$| ^ |$\le 2 \times 10^5$|一、三|
|$7$|$10$| ^ | ^ |一|
|$8$|$10$| ^ | ^ |无|
|$9$|$15$| ^ | ^ |^|
性质一:所有 $\texttt{1}$ 操作(修改)在所有 $\texttt{2}$ 操作(询问)之前。
性质二:任何时刻保证树是一条链。
性质三:最终形成的树在所有 $n$ 个点的有标号无根树中均匀随机,随机数生成器使用[梅森旋转算法](https://en.wikipedia.org/wiki/Mersenne_Twister)。
注意样例 3 满足性质一、二。