P14498 [NCPC 2025] Dune Dash

:::align{center}  A runner during a 15-kilometer run through the Grand Bara Desert in Djibouti. Public domain photo by Joshua Bruns. :::

You signed up for the $\emph{Dune Dash}$, a running race across the desert. Everything went well — except that in the excitement, you forgot to start $\emph{StrideTrack}$, the app that records how far you've run. All you have now are the official checkpoint locations, but not the order in which you passed through them. Formally, the race consisted of $N$ checkpoints, each given by its coordinates in the Euclidean plane. The sequence in which they were visited is unknown to you, but the organizers designed the course to prevent anyone from straying off route. In particular, if $q_1, q_2, \dots, q_N$ is the correctly ordered list of the checkpoints along the race, then for every triple $i < j < k$ it holds that $$\text{dist}(q_i, q_k) > \max(\text{dist}(q_i, q_j), \text{dist}(q_j, q_k) )$$ where $\text{dist}(p,q)$ denotes the Euclidean distance between points $p$ and $q$. Your task is to determine the total length of the race. 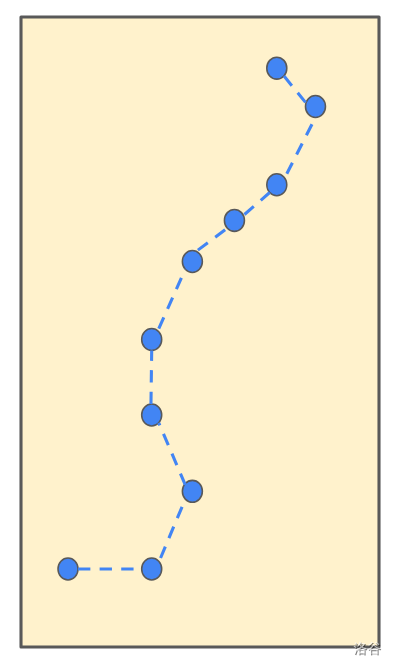:::align{center}  Illustration of sample 2. The dashed line shows where the race went. :::

The first line consists of the integer $N$ ($2 \leq N \leq 2 \cdot 10^5$). The following $N$ lines each contain two integers $x_i$ and $y_i$ ($-10^9 \leq x_i, y_i \leq 10^9$). These are the coordinates of each checkpoint. The checkpoints are not necessarily in the order in which they were visited during the race. It is guaranteed that there is some ordering of the checkpoints such that they satisfy the distance requirements above. The $N$ points given in the input are all distinct.

Print one floating point number, the length of the race. Your answer will be correct if it has an absolute or relative error of at most $10^{-6}$.