P14503 [NCPC 2025] Instagraph

:::align{center}  ::: A celebrity in a social network is somebody with many followers, but who doesn't follow them back. More precisely, a person is a $\emph{celebrity}$ for a group of people, if - every member of the group follows the person, - the person follows nobody in the group. The $\emph{celebrity centrality}$ of person $v$, written $\mathrm{CC}(v)$, is the maximum size of such a group. We model the social network as a directed graph with $N$ vertices $1$, $\ldots$, $N$. A directed edge from $u$ to $v$ means that person $u$ follows person $v$. 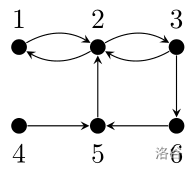For example, in :::align{center}  ::: we have $\operatorname{CC}(1) = 0$, $\operatorname{CC}(2) = 1$, and $\operatorname{CC}(5) = 2$. Your task is to find a vertex $v$ with the maximum celebrity centrality $\mathrm{CC}(v)$. In case of a tie, choose the smallest $v$.

The input consists of - One line with two integers $N$ and $M$ ($1 \le N \le 200\,000$, $0 \le M \le 1\,000\,000$), the number of vertices and the number of directed edges. - $M$ lines with two distinct integers $u$ and $v$ ($1 \le u,v \le N$), indicating a directed edge from $u$ to $v$. There are no duplicate edges.

Output two integers: the smallest $v$ with the maximum celebrity centrality and the value $\mathrm{CC}(v)$.