P14503 [NCPC 2025] Instagraph

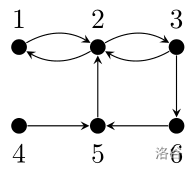
:::align{center}  ::: 在社交网络中，衡量“名人”的一个方式是：他们有很多关注者，但并不会回关这些人。更精确地说，对于一组人而言，如果某人满足： - 组内的每个人都关注 TA； - TA 不关注组内的任何人； 那么此人就是该组的 **名人（celebrity）**。 某个人 $v$ 的 **名人中心性（celebrity centrality）**，记作 $\mathrm{CC}(v)$，是满足上述条件的最大组的大小。 我们将社交网络建模为一个有向图，图中共有 $N$ 个顶点 $1,\ldots,N$。存在从 $u$ 到 $v$ 的有向边表示：用户 $u$ 关注用户 $v$。例如，在下图中： :::align{center}  ::: 我们有 $\operatorname{CC}(1)=0$、$\operatorname{CC}(2)=1$、$\operatorname{CC}(5)=2$。 你的任务是找到一个顶点 $v$ 使其名人中心性 $\mathrm{CC}(v)$ 最大；若有多个答案，则输出其中编号最小的 $v$。

输入包含： - 一行两个整数 $N$ 与 $M$（$1 \le N \le 200\,000$，$0 \le M \le 1\,000\,000$），分别表示顶点数量与有向边数量； - 接下来 $M$ 行，每行包含两个不同的整数 $u$ 和 $v$（$1 \le u,v \le N$），表示存在一条从 $u$ 指向 $v$ 的有向边。不存在重复边。

输出两个整数：名人中心性最大的最小编号顶点 $v$，以及对应的值 $\mathrm{CC}(v)$。

翻译由 ChatGPT-5 完成