P14512 [NFLSPC #8] 数嘟嘟嘟嘟嘟
题目描述
数数数数数数数嘟一般由 $n$ 个 $\sqrt{n} \times \sqrt{n}$ 的 $n$ 宫格的宫组成。
每一直行和每一横横横横横横横列的数字均须包含 $1\sim n$,不能缺少,也不能重复复复复复复复。 每一宫(粗黑线围起来的区域,通常是 $\sqrt{n} \times \sqrt{n}$ 的 $n$ 宫格
)的数字均须包含 $1\sim n$ ,不能缺少少少少少少少少少少,也不能重重重重重重重重重重重复。 完成需同时满足这三个条件件件件件件件件件。
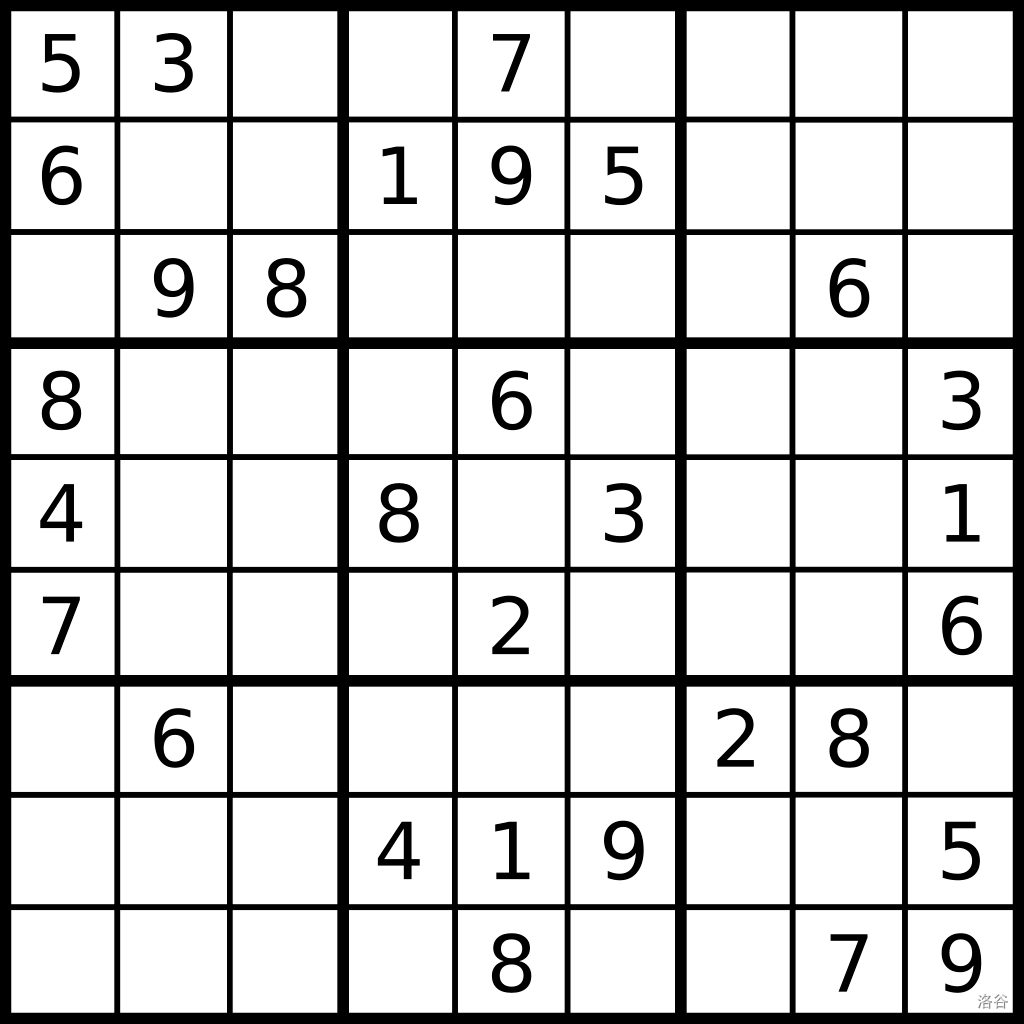
如图是一个 $n$ 宫格($n=9$)数嘟嘟嘟嘟嘟嘟嘟嘟嘟嘟的示例。
给定一个不完整的数嘟题面面面面面面面面面面面面面,要求补上任意数量的数字,使得补完以后的数嘟**恰好**有两个解,即有**唯二解**;且要求在所有这样的补法法法法法法法法法中,它所对应的唯二解差异最大大大大大大大大大大大。这里,差异定义为将两个解法逐单元格比对,不一样的数字个数。
**同时,对于数独中的任意两个位置,设 $x_1,x_2$ 表示两个唯二解在两个数独中第一个位置的数,$y_1,y_2$ 表示两个唯二解在两个数独中第二个位置的数,不同时满足 $x_1\not=x_2,y_1\not=y_2,x_1\not=y_2,x_1 \not = y_1$。**
输入格式
第一行,一个数 $n$ 表示数嘟大小。
接下来 $n$ 行,每行 $n$ 个数 ${a_i}_j$,表示一个不完整的数嘟题面,填数字 $0$ 的位置表示那里没有数数数数数数数数数数数。
输出格式
$n$ 行,每行各 $n$ 个数,输出补完以后的盘面,若有多种补法都可以满满满满满满满满满满满足其对应的唯二解差异在所有补法中最大,输出任意一种即可。
说明/提示
### 祥例解释
样例输出所对应的唯二解是:
```
3 2 1 4
1 4 3 2
4 3 2 1
2 1 4 3
```
和:
```
3 2 4 1
4 1 3 2
1 3 2 4
2 4 1 3
```
逐一比对可得差异为 $8$,可以证明,这是其中一种使得差异达到这个题面的最大值值值值值值值值值值值值值 $8$ 的方法。
### 数据范范范范范范范范范围
|子任务编号|数据点编号|分值|数据范围|额外限制|时间限制|
|:--:|:--:|:--:|:--:|:--:|:--:|
|1|1|8|$n=4$| 无无无无无无无无无无无无无无 |2s|
|^|11|^|^| ^ |^|
|^|12|^|^| ^ |^|
|^|13|^|^| ^ |^|
|2|2|6|$n=9$| 初始给定数字数量为 $0$ |25s|
|^|3|^|^| 保证盘面至多给出 $11$ 个不为 $0$ 的数|^|
|^|4|^|^| ^|^|
|^|5|^|^| ^|^|
|^|6|^|^| ^|^|
|^|7|^|^| ^|^|
|^|8|^|^| ^|^|
|^|9|^|^| ^|^|
|^|10|^|^| ^|^|
|3|14|7|$n=16$| 初始给定数字数量为 $0$|^|
|4|15|^|^| 保证盘面至多给出 $20$ 个不为 $0$ 的数|^|
对于所有数据:$a_{i,j} \in [0,n]$,保证给出的不完整数嘟题面至少存在一种补法使得其有唯二解。
::::info[测试点 14]
```
16
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
```
::::
::::info[测试点 15]
```
16
0 0 10 0 0 0 0 1 0 0 0 0 0 0 0 16
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 16 0 0 0 0 0 0 0 0 0 0 2 0 0
0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0
0 0 0 0 9 0 0 0 0 0 0 0 0 7 0 0
7 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 15 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 7 0 0 0 0 0 0 0 0 0 0 0 9 0
0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 0
13 0 0 0 0 0 0 0 0 0 8 0 0 0 12 11
```
::::