P14533 [RMI 2018] 松鼠 / Squirrel
题目背景
翻译来自于 [LibreOJ](https://loj.ac/p/5128)。
本题时限相较原时限翻倍。
题目描述
**题目译自 [Romanian Master of Informatics 2018](https://rmi.lbi.ro/rmi_2018/) Day2 T2 「[Squirrel](https://rmi.lbi.ro/rmi_2018/_dwl/public.zip)」**
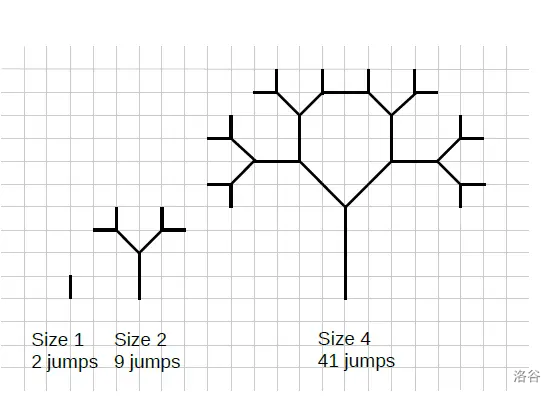
你站在一个 $M \times N$ 的树林网格的左上角,坐标为 $(1,1)$。一只松鼠在树间跳跃。作为一只计算机科学松鼠,它以特定的方式跳跃,形成了……树的分形图案!这些 $S$ 分形图案如图所示:
:::align{center}
:::
:::align{center}
:::
松鼠遵循以下规则:
- 松鼠从一棵指定的树开始跳跃。
- 它首先向北跳跃 $P$ 棵树,其中 $P$ 是给定的 $2$ 的幂。
- 然后,它沿两条长度为 $P/2$ 的对角线跳跃。
- 接着,它形成四个大小为 $P/2$ 的分形。
- 这一过程持续进行,直到创建出大小为 $1$ 的分形。
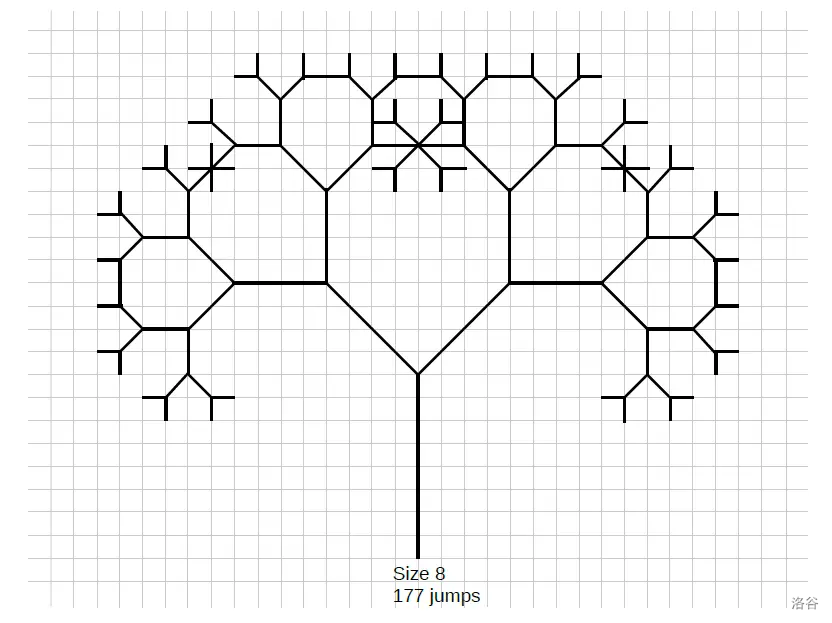
- 图中展示了大小为 $1$、$2$、$4$ 和 $8$ 的前四个分形。
松鼠会持续跳跃,直到完成一个分形图案,然后开始下一个分形。你想知道在多少棵树上可以看到这只松鼠?
输入格式
第一行包含三个整数 $M, N, F$,分别表示树林网格的行数、列数和分形数量。接下来的 $F$ 行描述 $F$ 个分形,每行包含三个整数,表示起始树的坐标以及分形大小。
输出格式
输出一个整数,表示可以看到松鼠的树的位置数量。
说明/提示
### 样例 1 解释
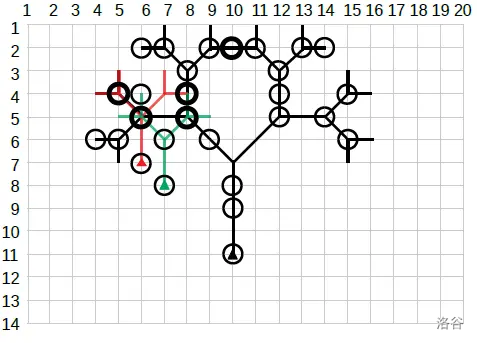
在样例中:
- 树林网格有 $14$ 行 $20$ 列。
- 松鼠跳跃三个分形,分别标记为黑色、红色和绿色。
- 三角形标记分形的起点。
- 圆圈标记从坐标 $(1, 1)$ 可见的树。
- 较粗的圆圈标记松鼠多次跳跃的可见树。
- 在可见树上的总跳跃次数为 $35$。
:::align{center}
:::
### 数据范围
对于所有输入数据,满足:
- 如果你和松鼠所在树之间没有其他树阻挡,你可以看到松鼠。
- 松鼠完成当前分形的所有跳跃后停止,然后开始下一个分形。
- 松鼠永远不会跳到你的位置 $(1,1)$。
- 松鼠永远不会跳出树林网格。
- 如果松鼠多次跳到同一棵可见的树上,该树将多次计入最终结果。
- $2 \leq M, N \leq 50000$
- $1 \leq F \leq 1000$
- $1 \leq$ 分形大小 $\leq 1024$,分形大小为 $2$ 的幂
- 总跳跃次数最多为 $3\times 10^8$
每个测试点将单独评分。
| 子任务 | 分值 | 附加限制 |
| :----: | :----: | :-------: |
| $1$ | $15$ | 总跳跃次数最多为 $4 \times 10^7$ |
| $2$ | $10$ | 总跳跃次数最多为 $6.5 \times 10^7$ |
| $3$ | $25$ | 总跳跃次数最多为 $1.25 \times 10^8$ |
| $4$ | $50$ | 无附加限制 |