P14537 [OII 2025] 双色金字塔 / Piramide bicolore
题目背景
译自 [Italian Olympiad in Informatics (OII) 2025 - Piramide bicolore](https://training.olinfo.it/task/oii_concessione)。
建造 OII 纪念金字塔的准备工作一切就绪,现在轮到 Nicoletta 向乌迪内市议会提交项目方案了。
题目描述
金字塔由黑色和白色的立方体构成。为了加快进度,项目按以下方式执行:
1. 首先,Nicoletta 将设计底座(第 $0$ 层):这一层是一个 $N \times N$ 的立方体方阵,其颜色可以用矩阵 $M$ 描述。具体来说,如果 $M_{i,j} = 1$,$(i, j)$ 上的立方体就是黑色,否则是白色的。
2. 然后,她将继续建造第 $1$ 层到第 $N - 1$ 层。第 $i$ 层的每个立方体都**恰好位于其下方四个立方体的公共顶点之上**。如果在它下方的四个立方体中,**相邻**的立方体都不同色,这个立方体就是黑色,否则是白色的。
:::align{center}
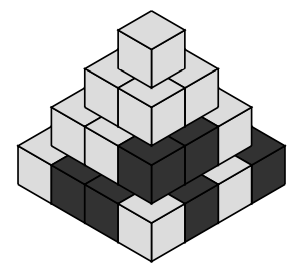
*图 1:Nicoletta 提出的金字塔方案之一。*
:::
市议会对该项目仍不完全信服,并希望获得有关金字塔最终外观的更多信息。为了更清楚地了解情况,议会决定向 Nicoletta 提出 $Q$ 个问题:在每个问题中,他们会询问位于第 $h$ 层、位置 $(x, y)$ 的立方体是什么颜色。
> 金字塔中的立方体可由一个三元组 $(h, x, y)$ 表示,其中 $0 \le h < N$ 是立方体的层数,$0 \le x, y < N - h$ 是其在层内的坐标。特别地,立方体 $(h, x, y)$ 恰好位于其下方四个立方体的公共顶点之上:$(h - 1, x, y)$、$(h - 1, x + 1, y)$、$(h - 1, x, y + 1)$ 和 $(h - 1, x + 1, y + 1)$。在样例解释中你可以看到一个示例。
### 实现方式
附件中包含一个实现示例 `concessione.cpp`。
你需要实现如下函数:
```cpp
void init(int N, vector M);
```
* $N$:金字塔的大小。
* $M$:二维数组,每一维下标从 $0$ 到 $N - 1$,表示金字塔的第 $0$ 层(底座)。
* 对于每个测试点,该函数都只会被调用一次。
```cpp
bool query(int h, int x, int y);
```
* 整数 $h,x,y$ 表示立方体的位置是 $(h,x,y)$。
* 如果位置 $(h, x, y)$ 上的立方体是黑色的,则该函数需要返回 `true`;否则返回 `false`。
* 对于每个测试点,该函数将被调用 $Q$ 次。
输入格式
评测程序的输入格式如下:
* 第 $1$ 行:两个整数 $N$ 和 $Q$。
* 第 $2 + i$ 行($0 \le i < N$):一个只包含字符 `0` 和 `1` 的字符串 $S$,表示 $M_{i,j} = S_j$。
* 第 $2 + N + i$ 行($0 \le i < Q$):三个整数 $h_i, x_i, y_i$。
输出格式
评测程序的输出格式如下:
输出包含 $Q$ 行,内容为 `query` 函数返回的值。
说明/提示
#### 【样例解释】
该图展示了第一个样例:
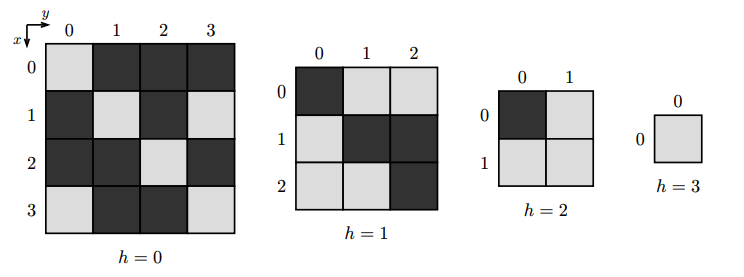
位置 $(1, 0, 0)$ 上的立方体是黑色的,因为它下方的四个立方体中,相邻的立方体都不同色。
位置 $(2, 0, 1)$ 上的立方体是白色的,因为它下方的立方体 $(1, 0, 1)$ 和 $(1, 0, 2)$ 相邻且同色。
#### 【数据范围】
* $1 < N \le 5000$;
* $1 \le Q \le 10^6$;
* 对于所有的 $0 \le i, j < N$,$M_{i,j} \in \{0, 1\}$;
* 对于每次询问,$1 \le h < N$, $0 \le x, y < N - h$。
#### 【子任务】
| 子任务编号 | 分值 | 约束条件 |
| :----: | :--: | :------: |
| $0$ | $0$ | 样例 |
| $1$ | $10$ | $N \le 300$ |
| $2$ | $21$ | 当 $i \ne j$ 时 $M_{i,j} = 0$,即底座中的黑色立方体全在一条对角线上 |
| $3$ | $28$ | $Q = 1$ 且仅询问金字塔塔尖的颜色 |
| $4$ | $12$ | $Q \le 100$ |
| $5$ | $29$ | 无额外限制 |