P14577 Magnetic Pole Conversion

Every performance might well be the last…

Morey specializes in magnets. In the course of the research, Morey has manufactured magnets made of $26$ different materials, denoted by the lowercase Latin letters. Morey has implemented a spectacular technique. First, all the magnets are laid out in a row. When a button is pressed, then for each material type separately, the 1st, 3rd, 5th, ... occurrences become north-poles (N), and the 2nd, 4th, 6th, ... occurrences become south-poles (S). Then, for each material separately, for each positive integer $k$, the $(2k-1)$-th and the $(2k)$-th magnets of that material attract each other and move toward each other until they collide—if both exist. During the collision, all magnets in the interval between them (inclusive) are destroyed. All such collisions happen simultaneously. In addition, the $i$-th magnet has an associated value $a_i$. If we represent the sequence of magnet materials by a string $S$, we denote by $f(S)$ the sum of the values of the magnets that remain after applying this technique. Now, there are $n$ magnets placed in the machine in positions $1$ through $n$. You are given their material types and values. Morey wants to process two types of operations: Update: Change the value of a single magnet. Query: For a given index interval $[l,r]$, apply the technique only to the magnets in that interval, and report the sum of the values of the magnets that remain in that interval, i.e. $f(S_{[l,r]})$. Formally, the operations are: - `1 x y`: Set $a_x \gets y$. - `2 l r`: Output $f(S_{[l,r]})$.

The first line contains a positive integer $n$, the number of magnets. The second line contains a string $S$ of length $n$, consisting of lowercase letters, where $S_i$ is the material of the $i$-th magnet. The third line contains $n$ integers $a_1, a_2, \dots, a_n$, the initial values of the magnets. The fourth line contains a positive integer $q$, the number of operations. Each of the next $q$ lines contains three integers describing one operation as above.

For each query, output one line containing the integer $f(S_{[l,r]})$.

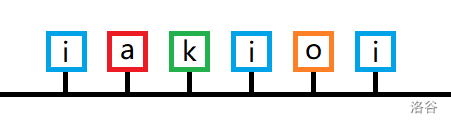
**Hint: Please use faster input/output methods.** ### Explanation of Examples  For Sample 1: - Query $[1,6]$: Material `i` occurs at positions $1, 4, 6$. Magnets at positions $1$ and $4$ attract and collide, destroying everything between them (i.e., positions $[1,4]$). Only magnets at positions $5$ and $6$ remain , so the remaining sum is $-5 + 3 = -2$. - Query $[3,6]$: Material `i` occurs at positions $4$ and $6$. Magnets at positions $4$ and $6$ attract and collide, destroying everything between them (i.e., positions $[4,6]$). Only magnets at positions $3$ remains with value $2$. For Sample 2: Magnets at positions $1$ and $4$ attract and collide, destroying everything between them (i.e., positions $[1,4]$). Meanwhile, Magnets at positions $2$ and $5$ attract and collide, destroying everything between them (i.e., positions $[2,5]$). Only position $6$ remains. | Subtask | $n \le$ | $q \le$ | Special Properties | Score | Time Limit | | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | | Subtask 1 | $1000$ | $1000$ | None | $10$ | 0.6s | | Subtask 2 | $10^4$ | $10^4$ | None | $10$ | 0.6s | | Subtask 3 | $2\times 10^5$ | $2\times 10^5$ | A | $20$ | 1.2s | | Subtask 4 | $2\times 10^5$ | $2\times 10^5$ | None | $20$ | 1.2s | | Subtask 5 | $5\times 10^5$ | $5 \times {10}^5$ | B | $30$ | 1.2s | | Subtask 6 | $5\times 10^5$ | $5\times 10^5$ | None | $10$ | 1.2s | Special Property A: $S$ contains only the first $8$ letters of the alphabet. Special Property B: There are no update operations. For all data, $1 \le n,q \le 5\times10^5$, $|a_i| \le 10^9$, and $S$ consists only of lowercase Latin letters.