P14587 [LNCPC 2025] 广义菊花图计数
题目背景
Z 形管道猫种菊花,Z 形管道猫数菊花。
题目描述
给定 $n$ 个节点,标号为 $i$ 的节点具有权值 $a_i$。
定义一张广义菊花图是一棵满足“度数为 $1$ 的节点的数量大于等于度数最大的节点的**权值**”的**有标号无根树**。特别地,当存在多个度数最大的节点时,取它们的最大的权值。
请您求出这 $n$ 个节点构成一张广义菊花图的方案数 $^{\text{*}}$,结果对 $998244353$ 取模。
**请注意次数过多的取模运算会带来较大的性能开销,请减少不必要的取模运算!**
---
$^{\text{∗}}$ 两张广义菊花图不同(也即两棵有标号无根树不同),当且仅当存在两个标号 $u,v$,标号为 $u$ 的节点和标号为 $v$ 的节点在一张广义菊花图上有边相连,在另一张广义菊花图上没有边相连。
输入格式
每个测试点包含多组测试数据。第一行给定一个整数 $T(1 \le T \le 50)$,表示测试数据组数。
对于每组测试数据:\
第一行给定一个整数 $n(3\le n\le250)$,表示节点总数。\
第二行给定 $n$ 个整数 $a_1, a_2, \dots, a_n(1\le a_i\le n)$,其中第 $i$ 个整数 $a_i$ 表示标号为 $i$ 的节点的权值。
保证在每个测试点中所有测试数据的 $n$ 的总和不超过 $250$。
输出格式
对于每组测试数据,输出一行一个整数,表示这 $n$ 个节点构成一张广义菊花图的方案数对 $998244353$ 取模后的结果。
说明/提示
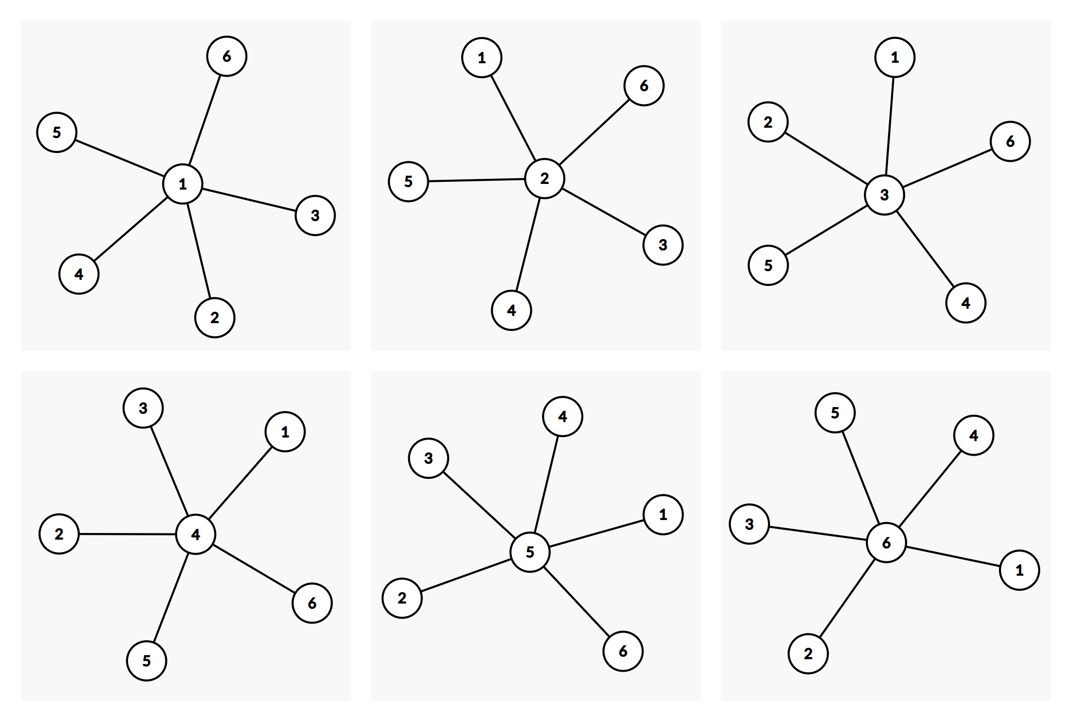
对于样例的第一组测试数据,这 $6$ 个节点构成一张广义菊花图的所有方案如下:
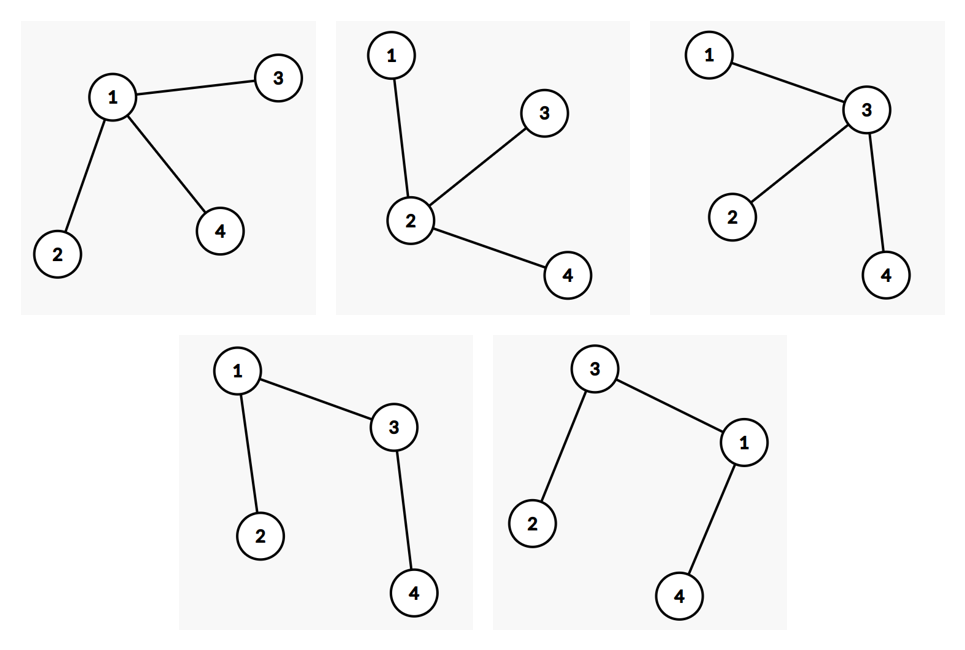
对于样例的第二组测试数据,这 $4$ 个节点构成一张广义菊花图的所有方案如下: