P14617 [2019 KAIST RUN Fall] Hilbert' s Hotel

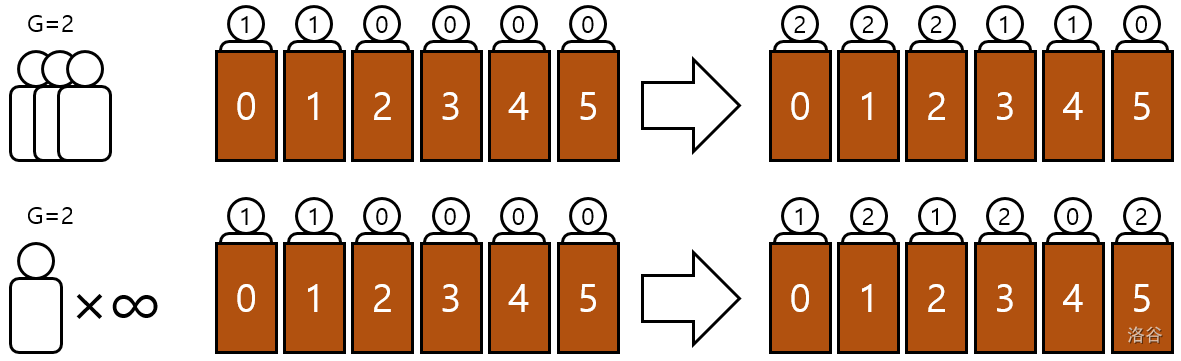
希尔伯特旅馆拥有无限多个房间，编号为 0, 1, 2, ... 每个房间最多住一位客人。由于人们倾向于团体入住，旅馆有一个团体计数器变量 $G$。 希尔伯特旅馆今天盛大开业。不久之后，无限多人同时到达，住满了旅馆的每个房间。所有客人都获得了团体编号 0，并且 $G$ 被设置为 1。 讽刺的是，即使每个房间都已住满，旅馆仍然可以接受更多客人： - 如果有 $k$（$k \geq 1$）个人到达旅馆，那么对于每个房间号 $x$，房间 $x$ 的客人移动到房间 $x+k$。之后，新客人填满从 0 到 $k-1$ 的所有房间。 - 如果有无限多个人到达旅馆，那么对于每个房间号 $x$，房间 $x$ 的客人移动到房间 $2x$。之后，新客人填满所有奇数编号的房间。 :::align{center}  ::: 你需要编写一个程序来处理以下查询： - $\tt{1\ k}$ - 如果 $k \geq 1$，那么 $k$ 个人到达旅馆。如果 $k = 0$，那么无限多个人到达旅馆。将团体编号 $G$ 分配给新客人，然后将 $G$ 增加 1。 - $\tt{2\ g\ x}$ - 找到包含团体编号为 $g$ 的客人的第 $x$ 小的房间号。输出其对 $10^9 + 7$ 取模的结果，然后换行。 - $\tt{3\ x}$ - 输出房间 $x$ 中客人的团体编号，然后换行。

第一行给出一个整数 $Q$（$1 \leq Q \leq 300,000$），表示查询的数量。接下来的每行包含一个查询。查询中的所有数字都是整数。 - 对于 $\tt{1\ k}$ 查询，$0 \leq k \leq 10^9$。 - 对于 $\tt{2\ g\ x}$ 查询，$g < G$，$1 \leq x \leq 10^9$，并且至少有 $x$ 个客人的团体编号为 $g$。 - 对于 $\tt{3\ x}$ 查询，$0 \leq x \leq 10^9$。

处理所有查询并按需输出。保证输出不为空。

如果你了解“基数”的概念，请假设“无限”仅指“可数无限”。如果你不了解，则无需担心。 --- 翻译由 DeepSeek V3 完成