P14617 [2019 KAIST RUN Fall] Hilbert' s Hotel

Hilbert's hotel has infinitely many rooms, numbered 0, 1, 2, ... At most one guest occupies each room. Since people tend to check-in in groups, the hotel has a group counter variable $G$. Hilbert's hotel had a grand opening today. Soon after, infinitely many people arrived at once, filling every room in the hotel. All guests got the group number 0, and $G$ is set to 1. Ironically, the hotel can accept more guests even though every room is filled: - If $k$ ($k \geq 1$) people arrive at the hotel, then for each room number $x$, the guest in room $x$ moves to room $x+k$. After that, the new guests fill all the rooms from 0 to $k-1$. - If infinitely many people arrive at the hotel, then for each room number $x$, the guest in room $x$ moves to room $2x$. After that, the new guests fill all the rooms with odd numbers. 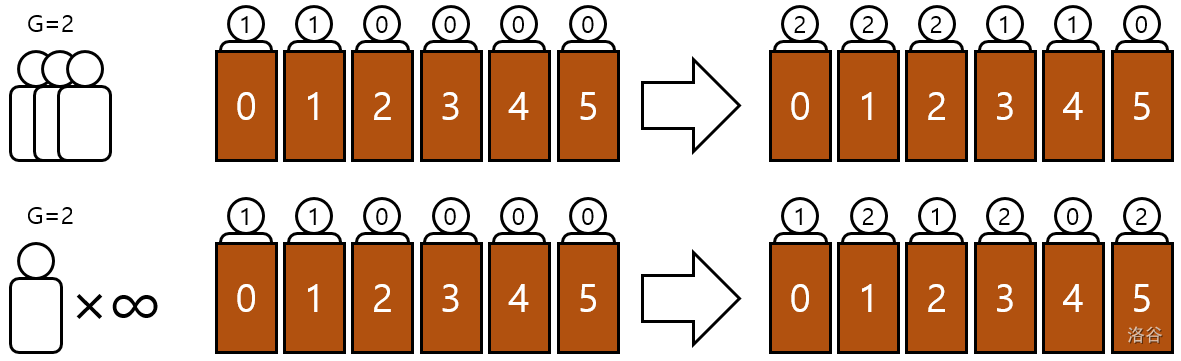:::align{center}  ::: You have to write a program to process the following queries: - $\tt{1\ k}$ - If $k \geq 1$, then $k$ people arrive at the hotel. If $k = 0$, then infinitely many people arrive at the hotel. Assign the group number $G$ to the new guests, and then increment $G$ by 1. - $\tt{2\ g\ x}$ - Find the $x$-th smallest room number that contains a guest with the group number $g$. Output it modulo $10^9 + 7$, followed by a newline. - $\tt{3\ x}$ - Output the group number of the guest in room $x$, followed by a newline.

In the first line, an integer $Q$ ($1 \leq Q \leq 300,000$) denoting the number of queries is given. Each of the next lines contains a query. All numbers in the queries are integers. - For the $\tt{1\ k}$ queries, $0 \leq k \leq 10^9$. - For the $\tt{2\ g\ x}$ queries, $g < G$, $1 \leq x \leq 10^9$, and at least $x$ guests have the group number $g$. - For the $\tt{3\ x}$ queries, $0 \leq x \leq 10^9$.

Process all queries and output as required. It is guaranteed that the output is not empty.

If you know about ``cardinals``, please assume that ``infinite`` refers only to ``countably infinite``. If you don't know about it, then you don't have to worry.