P14621 [2019 KAIST RUN Fall] Parklife

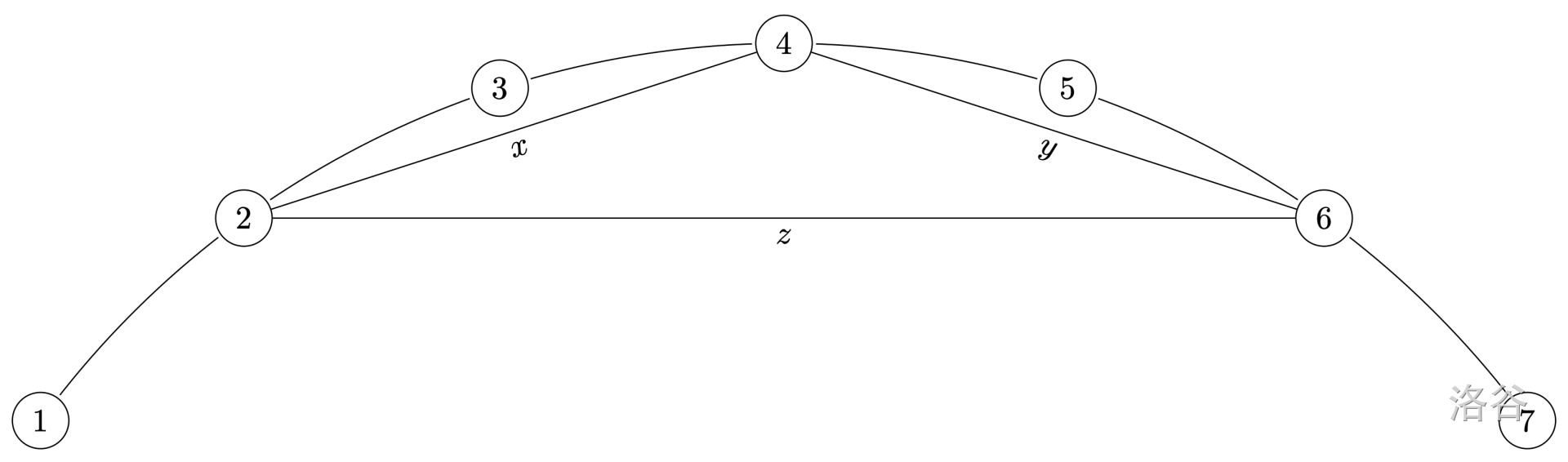
:::align{center}  阴天时的甲川和世博桥 ::: **甲川**（Gapcheon）是一条流经 **大德研发特区** 的溪流：这是大田市的一个研究区，包括韩国科学技术院（KAIST）、世博科学公园、国家科学博物馆等许多机构。甲川的滨水区被用作公园，是休闲娱乐的设施。 在这个问题中，我们将 **甲川** 建模为一个略微弯曲的弧形。在这个弧形中，每隔一厘米恰好标记了 $10^6$ 个点。在 **甲川** 上有 $N$ 座桥，每座桥以直线段连接弧上的两个不同点。这样的线段可能在端点处接触其他线段，但除此之外永远不会相交。对于任意一对点，最多存在一座桥直接连接这两个点。 :::align{center}  $x, y, z$ 是互不交叉但仅在端点处接触的桥。这是一个可能的输入实例。编号为 $8 \ldots 10^6$ 的点为简洁起见被省略。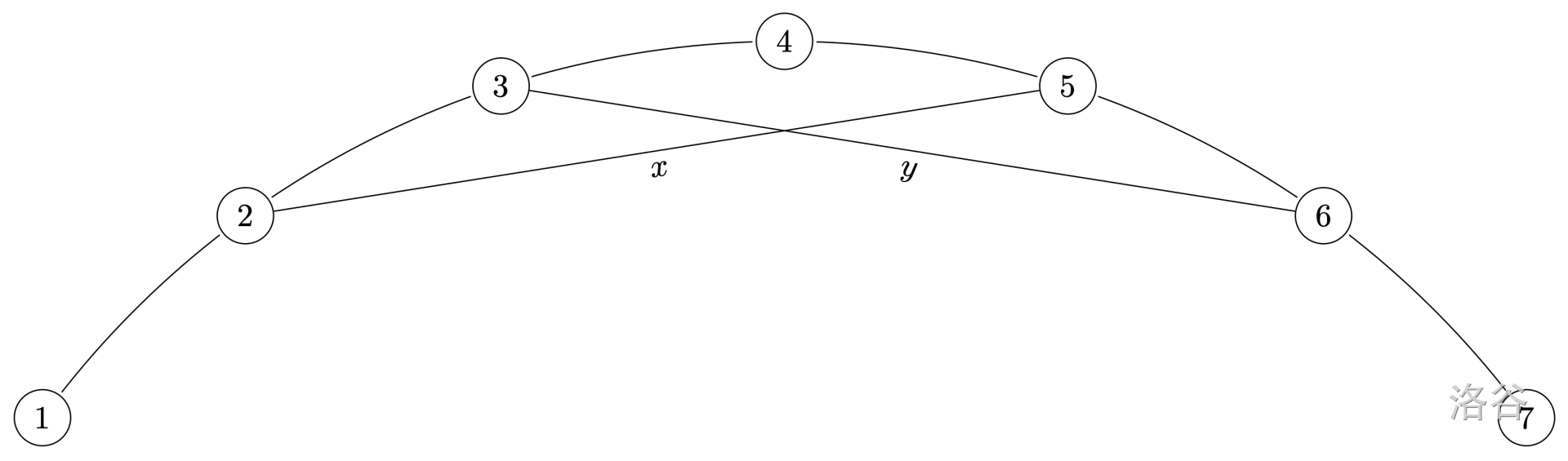 ::: :::align{center}  $x, y$ 是相互交叉的桥。这不是一个可能的输入实例。编号为 $8 \ldots 10^6$ 的点为简洁起见被省略。 ::: 市议会计划在桥上安装一些灯光，使甲川在夜晚成为更宜人的场所。对于每座桥，市议会计算了在这些桥上安装灯光的审美价值。这些价值可以用正整数表示。 然而，过多的灯光会在午夜打扰居民。为了解决这个问题，议会制定了一些规定：对于每两个相邻点之间的弧段，从该处可见的点亮桥梁最多为 $k$ 座。当一条线段的一个端点索引不大于 $i$，另一个端点索引不小于 $i+1$ 时，我们称该线段从连接 $i$ 和 $i+1$ 的弧段 **可见**。 市议会希望考虑光污染和夜景之间的权衡，因此你需要为所有整数 $1 \le k \le N$ 提供可能的最大审美价值总和。

第一行包含一个整数 $N$（$1 \le N \le 250,000$）。 接下来的 $N$ 行每行包含三个整数 $S_i, E_i, V_i$，表示存在一座直线桥连接点 $S_i$ 和 $E_i$，并具有审美价值 $V_i$（$1 \le S_i < E_i \le 10^6$，$1 \le V_i \le 10^9$）。 保证没有桥连接相同的点对，且没有两条不同的线段相交。

输出 $N$ 个以空格分隔的整数。第 $i$ 个整数（$1 \le i \le N$）应为 $k = i$ 时的答案。

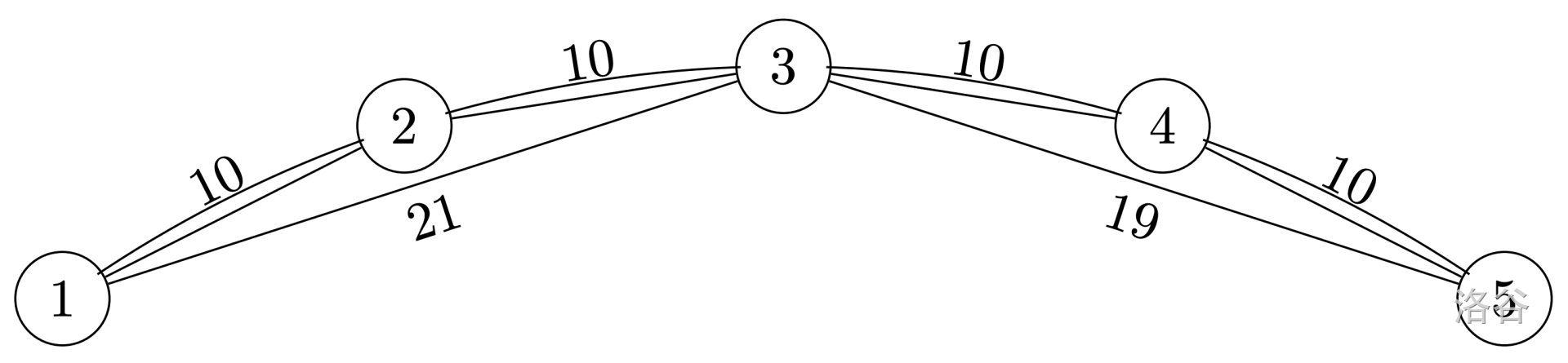
:::align{center}  样例输入 1 的图示。 ::: 图 1 的版权声明：사진제공(한국관광공사 김지호)-한국관광공사 --- 翻译由 DeepSeek V3 完成