P14626 [2018 KAIST RUN Fall] Fake Plastic Trees

**树** 是一种递归结构，它要么是： - **空树**。空树表示为 $-1$，大小为 $0$。 - **非空树**。非空树 $T$ 表示为一对树 $(T_1, T_2)$，其中 $T_1$ 称为 $T$ 的 **左子树**，$T_2$ 称为 $T$ 的 **右子树**。如果 $T = (-1, -1)$，则称这样的 $T$ 为 **叶子**。叶子的大小为 $1$，非叶子树的大小为 $|T_1| + |T_2|$，其中 $|T_1|$ 是 $T_1$ 的大小，$|T_2|$ 是 $T_2$ 的大小。 一棵非空树 $T$ 是 **虚假塑料树**，当且仅当该树是 **平衡的**。形式化地说，设 $T = (T_1, T_2)$。如果 $|T_1| = |T_2|$ 或 $|T_1| = |T_2| + 1$ 成立，则 $T$ 是虚假塑料树。 在计算机科学中，树通常被用作数据结构，并存储在内存中。最初，内存中没有树，只存在一个想象中的 **空指针**（对应空树 $-1$）。你可以通过将 $T_1$ 和 $T_2$ 设置为空指针或指向现有树的指针来在内存中分配一棵树。然后，内存通过将 $T = (T_1, T_2)$ 添加到其结构中来扩展。注意，指针可以用小整数描述，减少了显式存储整棵树的需要。 形式化地说，内存 $M$ 是一个归纳结构，最初只包含空树 $-1$（$M = \{-1\}$）。你可以通过以下操作扩展内存：$M \leftarrow M \cup \{(T_1, T_2)\}$，其中 $T_1 \in M, T_2 \in M$。如果一棵树 $T$ 在第 $i$ 阶段被插入，则它具有 **索引** $i-1$。对于索引为 $i$ 的树，它们的子树可以表示为范围在 $[-1, i-1]$ 内的一对整数。 你的任务是构造一个内存 $M$，满足以下条件： - $M$ 中的每棵树要么是空树，要么是虚假塑料树。 - $M$ 中最多有 $125$ 棵非空树。 - 存在一棵树 $T \in M$，满足 $|T| = N$。$N$ 是一个整数，作为输入给出。

第一行包含一个整数 $T$，表示测试用例的数量（$1 \leq T \leq 2000$）。 接下来的 $T$ 行，每行给出一个整数 $N$，表示你的树应包含的叶子数量（$1 \leq N \leq 10^{18}$）。

对于每个测试用例，你应该输出 $V + 2$ 行，其中 $V$ 是 $M$ 中非空树的数量（$1 \leq V \leq 125$）。 第一行输出一个整数 $V$。 接下来的 $V$ 行，每行输出两个以空格分隔的整数 $L_i, R_i$，表示索引为 $i$ 的树的左子树和右子树的索引（$-1 \leq L_i, R_i \leq i - 1$）。 第 $V+2$ 行输出 $P$，表示包含 $N$ 个节点的树的索引（$0 \leq P \leq V-1$）。 保证在给定条件下总是存在答案。

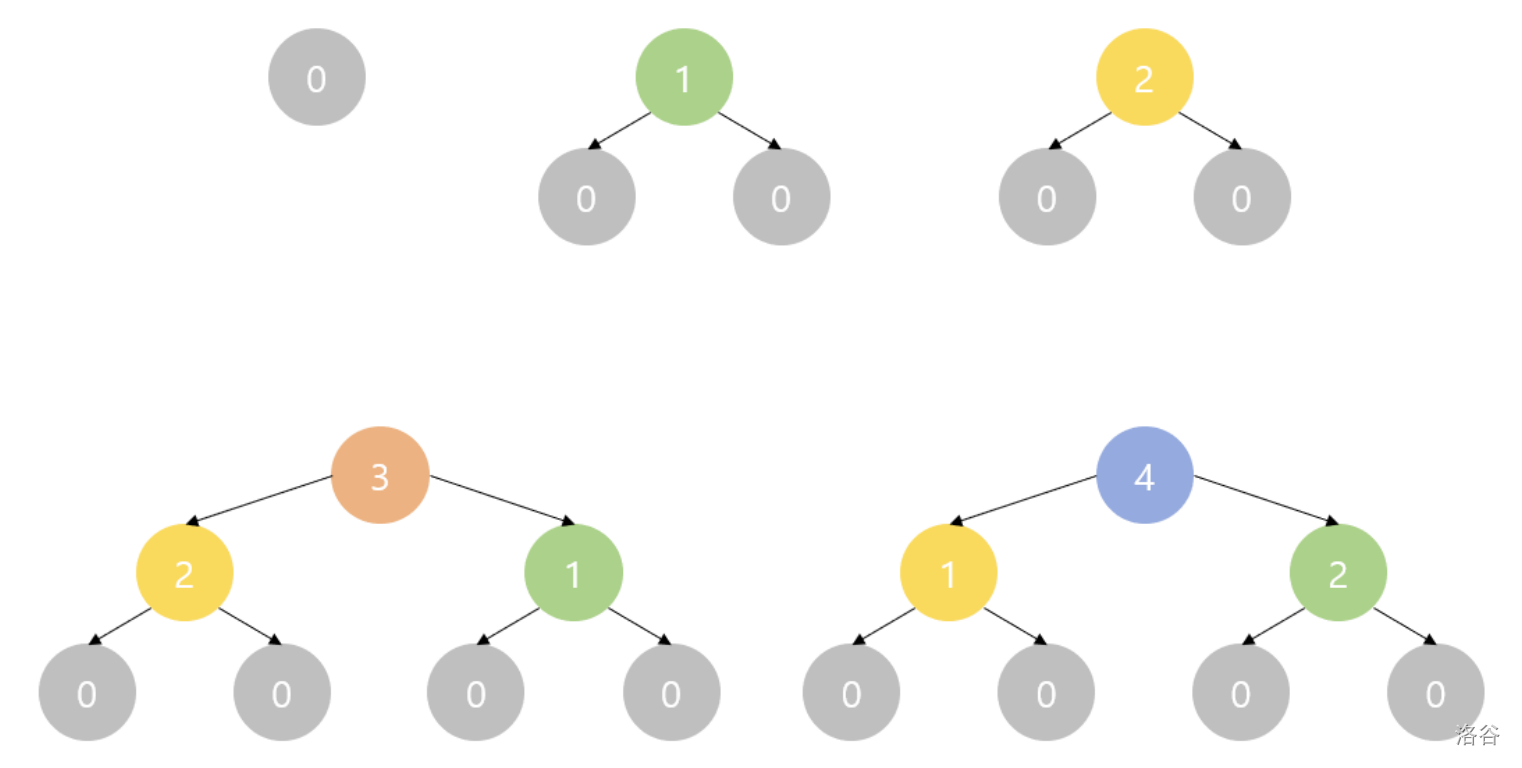
:::align{center}  示例中 $N = 4$ 的输出图示。 ::: --- 翻译由 DeepSeek V3 完成