P14630 [2018 KAIST RUN Fall] Histogram Sequence

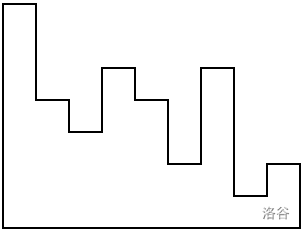
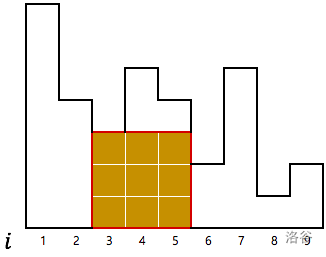
直方图是由 $N$ 个相邻矩形沿共同基线对齐形成的多边形。每个矩形称为一个 **条柱**。从左数第 $i$ 个条柱的宽度为 $1$，高度为 $H_i$。 :::align{center}  图示：此图描绘了 $N = 9$ 且 $H = [7,4,3,5,4,2,5,1,2]$ 的情况。 ::: 有一天，你想找出给定直方图中包含的最大矩形的面积。你通过以下步骤创建了一个整数列表 $A$： - 对于每个 $1 \le i \le j \le N$，计算直方图中包含的最大矩形面积，其中矩形的基线与第 $i, i+1, \cdots, j-1, j$ 个条柱的基线重合。将该面积添加到列表 $A$ 中。 :::align{center}  图示：此图描绘了 $i = 3$ 且 $j = 5$ 的情况。面积为 $9$。 ::: 列表 $A$ 的长度恰好为 $\frac{N(N+1)}{2}$，因为你恰好选择了每对 $(i, j)$ 一次。为了使生活更轻松，你将列表 $A$ 按非递减顺序排序。现在，要找到直方图中包含的最大矩形面积，你只需读取 $A$ 的最后一个元素 $A_{N(N+1)/2}$。 然而，你对此并不满意，所以我决定让你计算列表 $A$ 的某一部分。你需要编写一个程序，在给定两个索引 $L$ 和 $R$（$L \le R$）的情况下，计算 $A_{L..R}$ 的值，即 $A_{L}, A_{L+1}, \cdots, A_{R-1}, A_{R}$。

输入的第一行包含一个整数 $N$（$1 \le N \le 300,000$），表示直方图中条柱的数量。 下一行包含 $N$ 个以空格分隔的正整数 $H_1, H_2, \cdots, H_N$（$1 \le H_i \le 10^9$），其中 $H_i$ 是第 $i$ 个条柱的高度。 最后一行包含两个整数 $L$ 和 $R$（$1 \le L \le R \le \frac{N(N+1)}{2}$，$R - L + 1 \le 300,000$）。

输出 $R - L + 1$ 个整数。其中第 $j$ 个（$1 \le j \le R-L+1$）应为列表 $A$ 的第 $(L+j-1)$ 个元素，即 $A_{L+j-1}$。