P14630 [2018 KAIST RUN Fall] Histogram Sequence

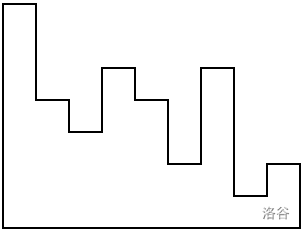
A histogram is a polygon made by aligning $N$ adjacent rectangles that share a common base line. Each rectangle is called a $\textit{bar}$. The $i$-th bar from the left has width 1 and height $H_i$. :::align{center}  Figure: This picture depicts a case when $N = 9$ and $H = [7,4,3,5,4,2,5,1,2]$. ::: One day, you wanted to find the area of the largest rectangle contained in the given histogram. What you did was to make a list of integers $A$ by the following procedure: - For each $1 \le i \le j \le N$, calculate the largest area of the rectangle contained in the histogram, where the rectangle's base line coincides with the base line of the $i, i+1, \cdots, j-1, j$-th bar. Add the area to the list $A$. 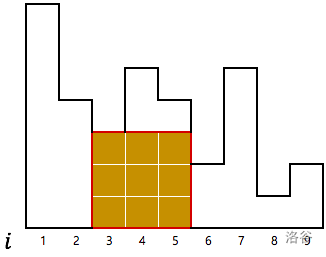:::align{center}  Figure: This picture depicts a case when $i = 3$ and $j = 5$. The area is 9. ::: The length of the list $A$ is exactly $\frac{N(N+1)}{2}$ since you chose each pair $(i, j)$ exactly once. To make your life easier, you sorted the list $A$ in non-decreasing order. Now, to find the largest area of the rectangle contained in the histogram, you just need to read the last element of $A$, $A_{N(N+1)/2}$. However, you are not satisfied with this at all, so I decided to let you compute some part of the list $A$. You have to write a program that, given two indices $L$ and $R$ ($L \le R$), calculate the values $A_{L..R}$, i.e. $A_{L}, A_{L+1}, \cdots, A_{R-1}, A_{R}$.

The first line of the input contains an integer $N$ ($1 \le N \le 300\,000$) which is the number of bars in the histogram. The next line contains $N$ space-separated positive integers $H_1, H_2, \cdots, H_N$ ($1 \le H_i \le 10^9$), where $H_i$ is the height of the $i$-th bar. The last line contains two integers $L$ and $R$ ($1 \le L \le R \le \frac{N(N+1)}{2}$, $R - L + 1 \le 300\,000$).

Print $R - L + 1$ integers. The $j$-th ($1 \le j \le R-L+1$) of them should be the $(L+j-1)$-th element of the list $A$, i.e. $A_{L+j-1}$.