P14632 [2018 KAIST RUN Fall] Rising Sun

Joon 明天有期中考试，但他什么都没学。因此他决定通宵学习。他承诺自己在太阳升起之前不会停止学习。 Joon 的家在山区。为方便起见，假设 Joon 生活在一个二维坐标系中。山区位于 $y \geq 0$ 的区域，起始于 $x = a_0$，其边界由 $2n$ 条分别平行于 $y = x$ 或 $y = -x$ 的线段组成。 更精确地说，山区的边界可以用 $(2n-1)$ 个额外的整数描述，其中第 $i$ 个数 $a_i$ 是山区第 $i$ 个尖顶的 $x$ 坐标。边界线从 $(a_0, 0)$ 开始，平行于 $y = x$ 延伸直到其 $x$ 坐标达到 $a_1$，然后平行于 $y = -x$ 延伸直到其 $x$ 坐标达到 $a_2$，依此类推。在最后一步之后，边界线平行于 $y = -x$ 延伸直到与 $x$ 轴相交。 山区的内部是边界下方且 $x$ 轴上方的区域。因此，内部与边界不相交。 在 $x = a_0$ 和 $x = a_{2n-1}$ 之间的某处，Joon 的家位于山区的边界上。与山区相比，他家的尺寸可以忽略不计。 目前，太阳位于原点，并以每分钟 $1$ 个单位的速度垂直（$+y$ 方向）上升。如果山区的内部不与连接 Joon 家和太阳的直线段相交，则 Joon 可以看到太阳。Joon 已经完全精疲力尽，想知道他何时可以停止学习。但如你所料，他已经神志不清，无法完成如此困难的数学计算。请帮助他！

输入的第一行包含一个整数 $n$（$1 \leq n \leq 10^3$）。 下一行包含 $2n$ 个整数，其中第 $i$ 个是整数 $a_{i-1}$（$1 \leq a_0 < \cdots < a_{2n-1} \leq 10^6$）。 最后一行包含一个整数 $x$，表示 Joon 家的 $x$ 坐标（$a_0 \leq x \leq a_{2n-1}$）。 保证山区的边界位于 $y \geq 0$ 的区域。

输出恰好一个整数 $m$，表示 Joon 在 $m$ 分钟后可以看到太阳的最小整数。

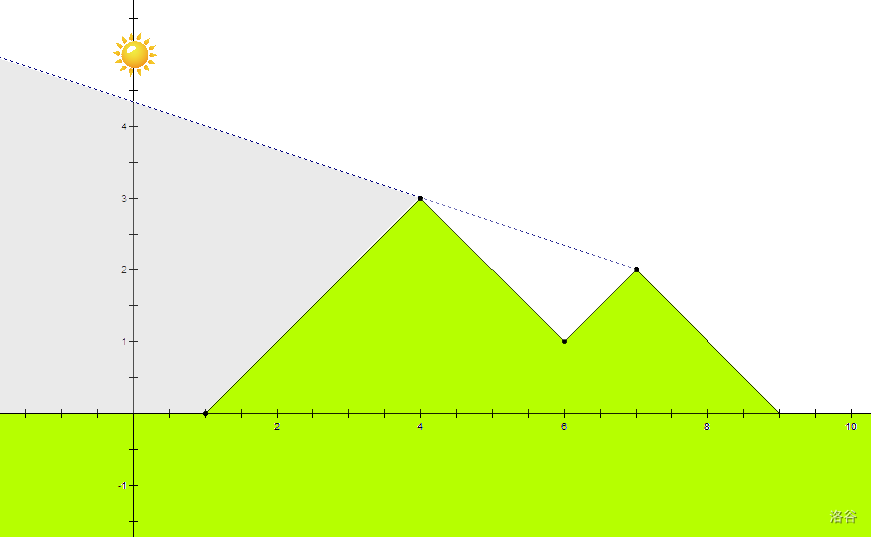
:::align{center}  第一个示例的图示。 ::: --- 翻译由 DeepSeek V3 完成