P14634 [2018 KAIST RUN Fall] Voronoi Diagram Returns

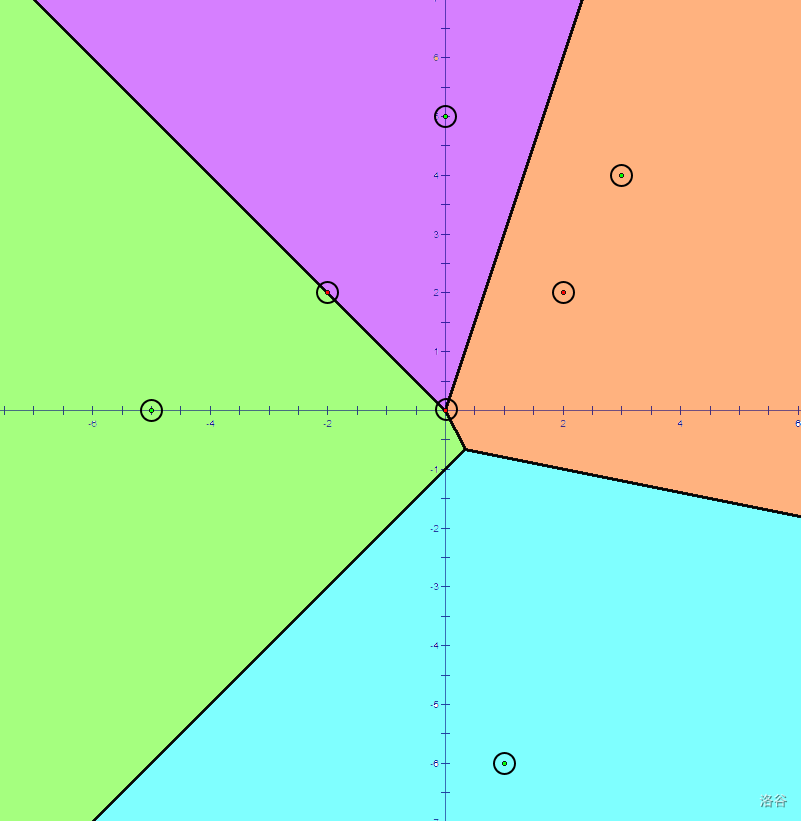
:::align{center}  大小为 4 的 Voronoi 图。 ::: 在二维笛卡尔坐标系中，我们将非空点集 $S$ 的 **Voronoi 图** 定义为按"该位置最接近集合 $S$ 中的哪个点？"这一准则划分平面的图形。更精确地说，给定非空点集 $\{P_1, P_2, \cdots, P_n\}$ 的 Voronoi 图是一个 **区域** 的集合：点 $K$ 包含在区域 $i$ 中当且仅当对于所有 $1 \le j \le n$ 有 $d(P_i, K) \le d(P_j, K)$，其中 $d(X, Y)$ 表示点 $X$ 和 $Y$ 之间的欧几里得距离。 例如，在上图中，平面上的每个位置都根据最接近的点着色。属于单个区域的点用浅色表示该区域，而属于多个区域的点形成黑色的线和点。 有一种算法可以在 $O(n \log(n))$ 时间内计算 Voronoi 图，但它以非常复杂和困难而闻名。实际上，我们是宽容的出题人，因此我们设定 $n \leq 2000$，这意味着你可以用较慢的 Voronoi 图算法解决这个任务！ 在此任务中，你需要解决 Voronoi 图中的 **点查询问题**：在由点集 $\{P_1, P_2, \cdots, P_n\}$ 构建的 Voronoi 图中，你需要确定点属于哪个（哪些）区域。更精确地说，你将收到 $q$ 个点的查询。对于每个查询点，你需要确定以下内容： - 如果它不包含在任何区域中，输出 `NONE`。 - 如果它恰好包含在一个区域中，输出 `REGION X`，其中 `X` 是该区域的索引。 - 如果它恰好包含在两个区域中，输出 `LINE X Y`，其中 `X` 和 `Y`（`X` $

第一行给出构成 Voronoi 图的点的数量 $n$ 和查询的数量 $q$（$3 \le n \le 2,000$，$1 \le q \le 250,000$）。 接下来的 $n$ 行中，第 $i$ 行给出两个整数，表示 $P_i$ 的 $x$ 和 $y$ 坐标。这些是构成 Voronoi 图的点。所有 $n$ 个点都是不同的（$|x|, |y| \le 10^4$）。 接下来的 $q$ 行中，第 $j$ 行给出两个整数，表示 $Q_j$ 的 $x$ 和 $y$ 坐标。对于每个点 $Q_j$，你应该确定给定点属于哪个（哪些）区域（$|x|, |y| \le 10^4$）。

输出包含 $q$ 行。在第 $j$ 行，你应该输出以下之一： - 如果 $Q_j$ 不包含在任何区域中，输出 `NONE`。 - 如果 $Q_j$ 恰好包含在一个区域中，输出 `REGION X`，其中 `X` 是该区域的索引。 - 如果 $Q_j$ 恰好包含在两个区域中，输出 `LINE X Y`，其中 `X` 和 `Y`（`X` $

示例图如上所示。 --- 翻译由 DeepSeek V3 完成