P14647 [POI 2025/2026 #1] 太空探测车 / Łazik kosmiczny

本题的可视化工具：[链接](https://oi.edu.pl/l/33oi_laz)（波兰语）。 Bajtazar 刚刚发现了一颗形状像环面的行星。行星表面被一个矩形网格划分为 $n$ 行和 $m$ 列。行用从 $0$ 到 $n-1$ 的整数编号，列用从 $0$ 到 $m-1$ 的整数编号，坐标为 $(x, y)$ 的格子位于第 $x$ 行和第 $y$ 列。 为了探索这颗行星，一辆太空漫游车将被送往那里，它将从坐标为 $(0, 0)$ 的格子开始工作，并按照指令序列在行星上移动。漫游车识别 4 种类型的指令，分别对应以下移动： * $G$：从 $(x, y)$ 移动到 $((x - 1) \bmod n, y)$ * $D$：从 $(x, y)$ 移动到 $((x + 1) \bmod n, y)$ * $L$：从 $(x, y)$ 移动到 $(x, (y - 1) \bmod m)$ * $P$：从 $(x, y)$ 移动到 $(x, (y + 1) \bmod m)$ 漫游车将无限循环地执行指令序列：在执行完最后一条指令后，它开始从头执行整个序列。请记住，行星的形状是环面，所以例如如果漫游车当前位于格子 $(x, 0)$ 并执行移动 $L$，它将移动到格子 $(x, m - 1)$。 Bajtazar 希望漫游车最终能访问行星上全部 $nm$ 个格子。请帮助他设计一个能保证这一点的简短（但不一定是最短）的指令序列。 注意，漫游车在行驶过程中多次访问同一个格子是允许的。

输入的第一行也是唯一一行包含两个整数 $n$ 和 $m$ ($2 \le n, m \le 10^6$)，分别表示行星表面被划分成的行数和列数。

输出的第一行应打印一个正整数 $k$，表示指令序列的长度。在第二行应打印一个长度为 $k$ 的由字母 $G, D, L, P$ 组成的字符串。

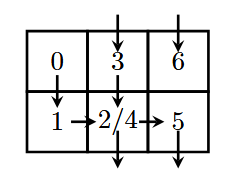
### 样例解释 漫游车依次访问格子 $$ (0,0) \xrightarrow{D} (1,0) \xrightarrow{P} (1,1) \xrightarrow{D} (0,1) \xrightarrow{D} (1,1) \xrightarrow{P} (1,2) \xrightarrow{D} (0,2) \xrightarrow{D} (1,2) \xrightarrow{P} (1,0) \xrightarrow{D} (0,0) \xrightarrow{D} \dots $$ ::::align{center}  :::: 样例输出是正确的，但未必是最短的。 ### 大样例 样例 $\texttt{0a}$ 是题面中展示的样例。此外： - $\texttt{0b}$：$n = 5, m = 4$；指令序列 $\texttt{PPPDDDLLGPGLLDDDPPP}$ 允许访问棋盘的所有格子。 - $\texttt{0c}$：$n = 1000, m = 1000$；指令序列 $(\texttt{DP})^{1\,234\,567}\texttt{GGL}$ 允许访问棋盘的所有格子。 ### 子任务 本题采用捆绑测试。 | 子任务编号 | 限制 | 得分 | | :---------: | :--------------------- | :-----: | | 1 | $n, m \le 6$ | 11 | | 2 | $n, m \le 20$ | 20 | | 3 | $n \le 10^3, n = 2m + 3$ | 13 | | 4 | $n \le 10^3, m \le 20$ | 12 | | 5 | $n, m \le 10^3$ | 24 | | 6 | $n, m \le 10^4$ | 7 | | 7 | $n, m \le 10^5$ | 7 | | 8 | 无额外限制 | 6 | 令 $k$ 表示你输出的指令序列的长度，而 $OPT$ 是最短可能的正确指令序列的长度。如果你的指令序列是正确的，那么你的解法将在该测试点获得根据以下公式计算的分数： $$ \left\lfloor \frac{100}{\sqrt{1 + k - OPT}} \right\rfloor \% $$