P14669 [ICPC 2025 Seoul R] Bay

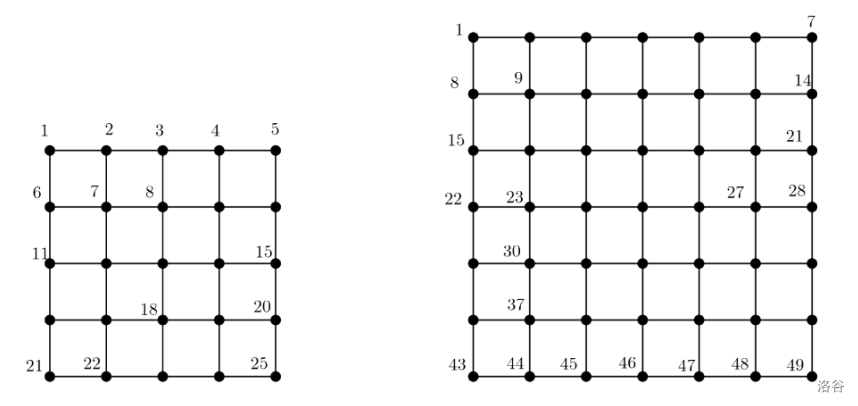
我们有一个网格（点阵）图 $G(n, n)$，其中 $n$ 是沿 $x$ 轴和 $y$ 轴的顶点数量，即行数和列数。图 $G(n, n)$ 的顶点按行优先顺序从 $1$ 到 $n^2$ 连续编号；从左上角的顶点开始，我们从上到下逐行遍历，在每一行内从左到右遍历。图 1 展示了两个带顶点编号的示例：$G(5, 5)$ 和 $G(7, 7)$。 :::align{center}  图 1. 左：网格图 $G(5, 5)$。右：$G(7, 7)$。 ::: 我们给定 $G(n, n)$ 的一棵生成树 $T$。图 2 左侧展示了 $G(7, 7)$ 的一棵生成树 $T$。如果我们添加一条不属于 $T$ 的 $G(n, n)$ 的边（称为非树边），那么恰好会创建一个简单环。我们将此环所围成的区域定义为一个 **湾**。非树边和湾之间存在一一对应关系，即每条非树边恰好对应一个湾。湾的面积定义为该环所围成的 $1 \times 1$ 单位方格的数量。图 2 右侧展示了通过分别添加两条非树边 $(u, v)$ 和 $(p, q)$ 所创建的两个湾（分别用蓝色和橙色标记）。注意，由 $(u, v)$ 和 $(p, q)$ 创建的两个湾的面积分别为 $4$ 和 $12$。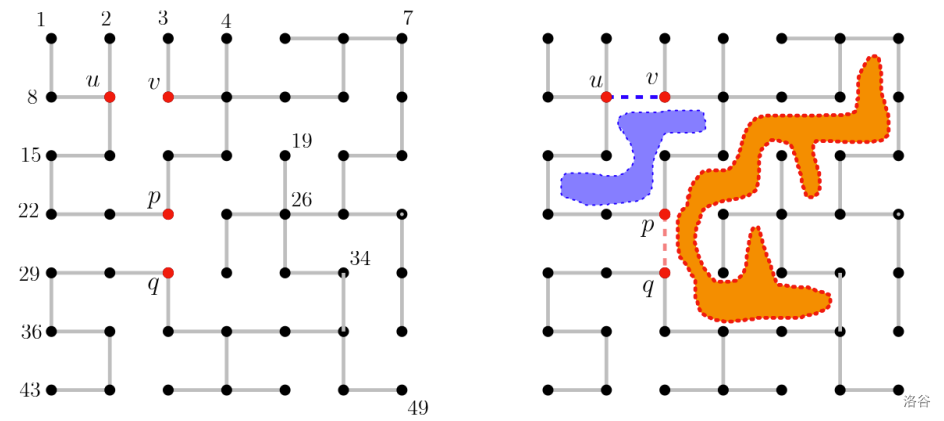 :::align{center}  图 2. 网格 $G(7, 7)$ 的一棵生成树 $T$ 以及由 $(u, v)$ 和 $(p, q)$ 创建的两个湾。 ::: 给定网格图 $G(n, n)$ 的一棵生成树 $T$ 和一个正整数 $S$，请编写一个程序，找出所有创建面积为 $S$ 的湾的非树边，并输出其中按字典序排列的第一条非树边。

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $n$ 和 $S$，其中 $5 \le n \le 300$ 对应于 $G(n, n)$，且 $1 \le S \le (n-1)^2$。接下来的 $n^2 - 1$ 行每行包含两个不同的整数 $u$ 和 $v$，表示生成树 $T$ 的一条边 $(u, v)$，其中 $1 \le u < v \le n^2$。

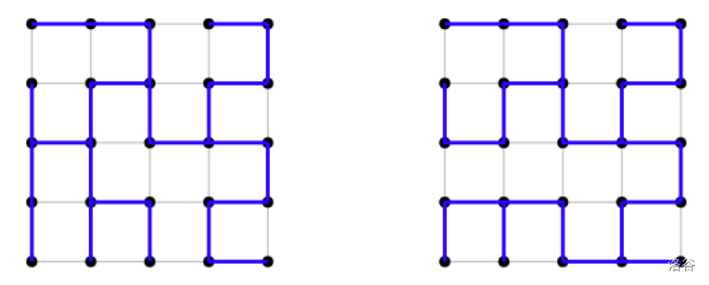
你的程序需要向标准输出写入数据。第一行应输出创建面积为 $S$ 的湾的非树边的数量。第二行应输出两个不同的整数 $u$ 和 $v$ ($u < v$)，表示在那些创建面积为 $S$ 的湾的非树边中，按字典序排列的第一条边 $(u, v)$。两条边 $(a, b)$ 和 $(c, d)$ 的字典序定义如下：当且仅当 $a < c$ 或 ($a = c$ 且 $b < d$) 时，$(a, b)$ 排在 $(c, d)$ 之前。如果没有创建面积为 $S$ 的湾的非树边，则第一行打印 "0"，第二行打印两个零 "0 0"。 图 3 展示了两个 $n = 5$ 的网格图的生成树，它们对应于样例输入和输出。 :::align{center}  图 3. $G(5, 5)$ 的两棵生成树，分别对应样例 1 和样例 2。 :::

翻译由 DeepSeek V3 完成