P14671 [ICPC 2025 Seoul R] Clean Arrangement

In graph drawing, a $linear\ arrangement$ of a rooted (connected) tree $T = (V, E)$ of $n$ vertices is a planar drawing where $n$ vertices of the tree are placed on a horizontal line, say the $x$-axis, and $(n-1)$ edges are drawn as semicircular arcs above the line connecting their end vertices as shown in Figure 1. Such linear arrangement $\pi$ maps each vertex to a distinct integer from $1$ to $n$, representing its coordinate along the $x$-axis. 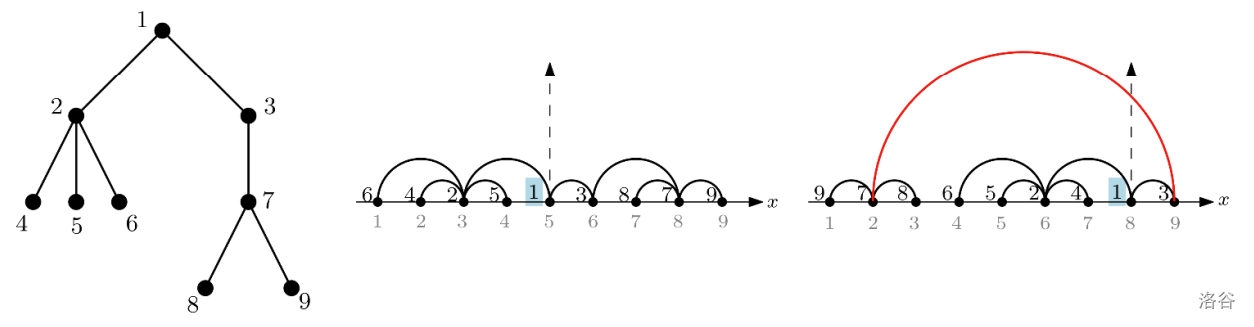:::align{center}  Figure 1. (Left) A rooted tree $T$ of nine vertices with the vertex 1 as a root.\ (Middle) A clean arrangement of $T$. \ (Right) An unclean arrangement of $T$ because of the red edge $(3,7)$ covering the root. ::: In a linear arrangement $\pi$, the distance $d(u, v)$ between two vertices $u$ and $v$ is defined as the difference of their $x$-coordinates, i.e., $d(u, v) = |\pi(u) - \pi(v)|$. Formally, for a rooted tree $T = (V, E)$, the cost of a linear arrangement $\pi$ of $T$ is defined as $\sum_{(u,v) \in E} d(u, v)$. A $clean\ arrangement$ $\pi$ of a rooted tree $T$ is a special linear arrangement $\pi$ satisfying both conditions: 1. $\pi$ has no edge crossings except at common end vertices of edges. 2. No edge covers the root vertex $r$ of $T$, that is, there is no edge $(u, v)$ such that $\pi(u) < \pi(r) < \pi(v)$. For example, the middle in Figure 1 is a clean arrangement of $T$ in the left, but the right is not clean because the edge $(3,7)$ covers the root vertex 1. The cost of the clean arrangement in the middle is 11, where there are three edges of distance two and five edges of distance one. This cost is the minimum among all clean arrangements of $T$. Given a rooted tree with the vertex 1 as a root, write a program to output the minimum possible cost of clean arrangements of the tree.

Your program is to read from standard input. The input starts with a line containing $n$ ($2 \le n \le 5,000$), where $n$ is the number of vertices of the rooted tree. The vertices are numbered from 1 to $n$, and the root vertex is 1. In the following $(n-1)$ lines, each line contains two positive integers $u$ and $v$ which are end vertices of an (undirected) edge $(u, v)$ of the tree, where $u$ and $v$ are distinct integers between 1 and $n$.

Your program is to write to standard output. Print exactly one line. The line should contain the minimum cost of clean arrangements of the tree with root vertex 1. The following shows sample input and output for two test cases. The second test case corresponds to Figure 1.