P14675 [ICPC 2025 Seoul R] Magic Door

:::align{center}  ::: 通往宝藏洞穴的魔法门是一个 $m \times n$ 的网格，其中布满了各种宝石。宝石分为三类：各种颜色和形状的**普通宝石**，以及两种特殊类型——**炸弹宝石**和**振金宝石**。 一个 **三消组** 是三个或更多相同的普通宝石在垂直或水平方向上连续对齐形成的组合。一个宝石可以同时属于一个水平三消组和一个垂直三消组，在这两个组的交点处。炸弹宝石不形成三消组。振金宝石也不形成三消组。 在网格的初始状态下，不存在任何三消组。当你最初用手触碰两个普通宝石时，它们会交换位置。这次单一交换会触发连锁反应，导致宝石根据一系列特定规则从网格中消失。 初始交换后，以下过程会重复进行，直到网格上不再发生任何变化： - **阶段 1：三消组的连锁反应** 1. 所有属于任意三消组的宝石同时消失。 2. 消失宝石上方的所有类型的宝石因重力下落，填充空位。在此过程中，任何向下移动至少一个格子的炸弹宝石变为**已激活**状态。 3. 如果宝石下落后形成了新的三消组，则本阶段从第一个子步骤重复。 4. 如果没有再形成三消组，则进入**阶段 2**。 - **阶段 2：已激活炸弹的引爆** 1. 所有当前处于**已激活**状态的炸弹同时爆炸。 2. 每个爆炸的炸弹向水平和垂直方向发射光束。 3. 光束从炸弹位置向网格边缘传播。 4. 光束的路径如果击中振金宝石则被阻挡。 5. 光束路径上的所有普通宝石和炸弹连同爆炸的炸弹一起消失。 6. 被光束击中的未爆炸炸弹仅消失而不爆炸。 7. 消失宝石上方的宝石因重力下落，填充新产生的空位。在此过程中，任何向下移动至少一个格子的炸弹变为**已激活**状态。然后**阶段 1** 重复。 一旦阶段 1 和阶段 2 不再引起任何变化，整个过程终止。请注意，炸弹宝石和振金宝石不会被初始交换选中，也不形成三消组。还需注意，振金宝石永远不会消失，它会作为阻挡炸弹光束的屏障，并且受重力影响会下落填充其下方的空位。 例如，考虑一个由 $6 \times 4$ 网格组成的魔法门，如图 1 所示。图中，$0$ 代表炸弹宝石，$-1$ 代表振金宝石，正整数代表普通宝石。从图 (a) 所示的初始状态开始，交换位于 $(6,1)$ 和 $(5,4)$ 的两个宝石，得到图 (b) 所示的状态。位置 $(r,c)$ 表示从上数第 $r$ 行、从左数第 $c$ 列的格子。坐标以 1 为起始。此状态包含一个由三个 $2$ 组成的三消组。根据阶段 1，当该组宝石消失时，达到状态 (c)。此时，位于 $(4,3)$ 的炸弹宝石被激活，并且形成了一个由三个 $1$ 组成的新三消组。再次执行阶段 1 移除三个 $1$，得到状态 (d)。由于没有剩余的三消组，炸弹因阶段 2 而爆炸。这导致状态 (e)。这里形成了两个三消组，分别由三个 $1$ 和四个 $3$ 组成。当这些宝石因阶段 1 再次消失后，达到状态 (f)。此状态下不再发生进一步变化，因此是最终状态。在此过程中，总共有 $18$ 颗宝石消失。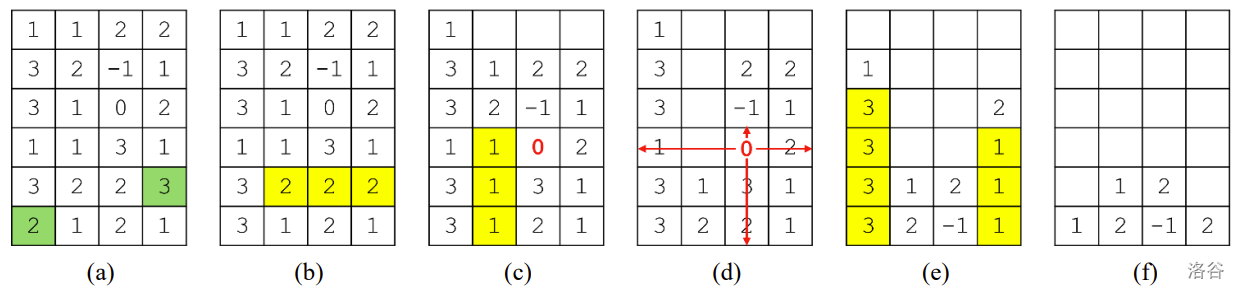 :::align{center}  图 1. 连锁反应 ::: 当特定数量的宝石消失时，魔法门会打开。你的任务是编写一个程序，在给定魔法门信息以及要交换的两个普通宝石的位置后，计算从单一交换开始并最终完全停止的整个连锁反应后，消失的宝石总数。

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $m$ 和 $n$ ($3 \le m \le 80$; $3 \le n \le 80$)，分别代表网格的行数和列数。接下来的 $m$ 行每行包含 $n$ 个整数，代表网格每行中的宝石，其中 $0$ 代表炸弹宝石，$-1$ 代表振金宝石，$1$ 到 $9$（含）之间的整数代表普通宝石。最后一行包含四个整数 $r_1, c_1, r_2, c_2$ ($1 \le r_1, r_2 \le m$; $1 \le c_1, c_2 \le n$)，其中 $(r_1, c_1)$ 和 $(r_2, c_2)$ 代表要交换的两个不同普通宝石的坐标。坐标以 1 为起始。

你的程序需要向标准输出写入数据。输出恰好一行。该行应包含一个整数，代表所有过程完成后将消失的宝石总数。

翻译由 DeepSeek V3 完成