P14677 [ICPC 2025 Seoul R] Quadrants

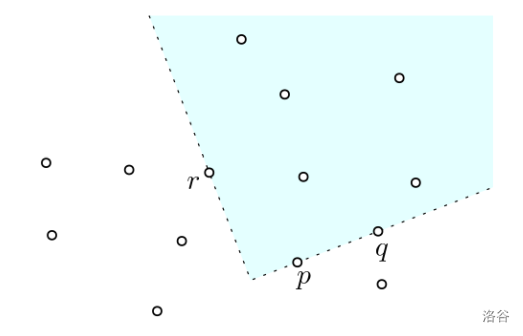
This problem is about **quadrants**. What are quadrants? Let us begin with any two perpendicular lines $\ell$ and $\ell'$ in the plane $\mathbb{R}^2$. If you subtract the two lines $\ell$ and $\ell'$ from the whole plane $\mathbb{R}^2$, you obtain four connected, unbounded regions. Each of the four regions is called a **quadrant**. Note that the boundary of a quadrant does not belong to itself. Now, consider a set $P$ of points in the plane $\mathbb{R}^2$. We are interested in quadrants defined by the set $P$ of points. Specifically, let $\mathcal{Q}$ be the set of quadrants $Q$ such that the boundary of $Q$ contains exactly three points of $P$. Each quadrant $Q \in \mathcal{Q}$ is called a $k$-quadrant if $Q$ contains exactly $k$ points of $P$ in its interior. The figure below shows an example in which the set $P$ consists of 14 points (small circles) and you can see a 5-quadrant $Q \in \mathcal{Q}$ (shaded in cyan), whose boundary contains three points $p, q, r \in P$. :::align{center}  ::: Given a set $P$ of $n$ points as input, write a program that computes the number of $k$-quadrants for every $0 \le k \le n-3$.

Your program is to read from standard input. The input starts with a line containing a single integer $n$ ($3 \le n \le 2,000$), where $n$ is the number of points in the input set $P$. In each of the following $n$ lines, given are two integers $x$ and $y$, both ranging from $-10^6$ to $10^6$, inclusively, that represent the $x$- and $y$-coordinates of an input point $(x,y)$ in $P$. You may assume that no two input points have the same coordinates, that there are no three points in $P$ lying in a line, and that there are no two perpendicular lines $\ell$ and $\ell'$ in the plane $\mathbb{R}^2$ such that $|\ell \cap P| \ge 2$ and $|\ell' \cap P| \ge 2$.

Your program is to write to standard output. Print exactly $n-2$ lines. The $i$-th line of your output for each $1 \le i \le n-2$ must contain a single integer that represents the number of $(i-1)$-quadrants with respect to the input set $P$ of $n$ points.