P14682 [ICPC 2025 Yokohama R] Seagull Population

一颗系外行星上的岛屿是著名的观鸟胜地，全年可以看到许多类似海鸥的鸟（以下简称海鸥）。这颗行星与地球非常相似，但一年的天数不同。 每只海鸥每年恰好来岛一次，停留一段时间，然后也恰好离岛一次。每只海鸥都有自己来岛和离岛的时间表，并且非常准时地遵守这个时间表。也就是说，每年，它都在一年中的同一天来到岛上。同样，每年，它也在一年中的同一天离开。海鸥在清晨来岛，傍晚离岛。已经来到岛上的海鸥可能在同一天离开。另一方面，海鸥可能在某一天离开岛屿，并在第二天再次来到。 观鸟俱乐部的成员们每天中午前后都会统计停留在岛上的海鸥数量。他们的统计是完美的，因此当时在场的所有海鸥都会被计入，没有遗漏或重复。然而，海鸥们看起来非常相似，无法识别个体。 请注意，那些在某天傍晚离岛并在第二天早上再次到来的海鸥，在一年中的所有日子里都会被计数。 给定一年中每天的海鸥计数，你想知道访问该岛的海鸥总数。由于海鸥无法区分，所以无法知道确切的数量。例如，如果连续两天的计数都是 $1$，那么海鸥的数量可能是 $1$ 或 $2$。你所能获得的唯一有价值的信息是可能的最小数量。 确定一年中至少被计数一次的海鸥个体的最小可能数量。如果这个最小值足够小，请同时展示一个能达到这个最小值可能的停留周期列表。

输入由单个测试用例组成，格式如下。 $$ n $$ $$ b_1 \ b_2 \ \cdots \ b_n $$ 整数 $n$ ($2 \le n \le 2 \times 10^5$) 是该行星上一年的天数。一年中的天数从 $1$ 到 $n$ 编号。整数 $b_i$ ($0 \le b_i \le 2 \times 10^5$) 是第 $i$ 天计数的海鸥数量。$b_i$ 中至少有一个非零。

第一行输出海鸥的最小可能数量 $m$。如果 $m$ 不大于 $2 \times 10^5$，则再输出 $m$ 行来描述一个可能的停留周期列表。这 $m$ 行中的第 $j$ 行应包含两个整数 $s_j$ 和 $t_j$ ($1 \le s_j \le n$, $1 \le t_j \le n$)，用一个空格分隔，表示第 $j$ 只海鸥在第 $s_j$ 天来岛，并在第 $t_j$ 天离开。注意 $s_j$ 可能大于 $t_j$。在这种情况下，海鸥会在岛上跨年停留，即从一年的最后一天到下一年的第一天。当存在两种或更多可能时，输出其中任何一种均可。

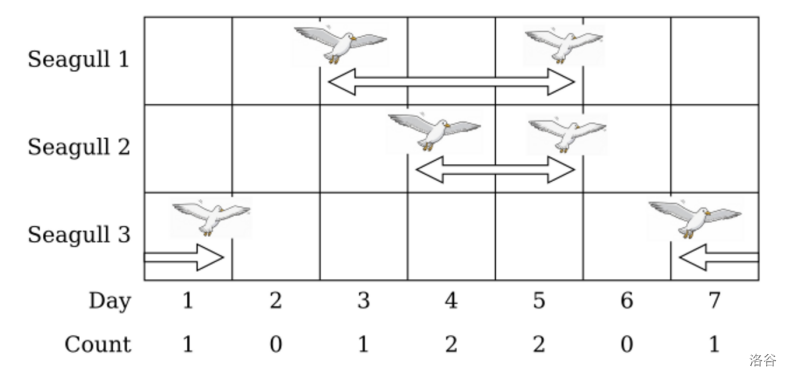
下图描绘了样例输出 1 中三只海鸥的访问时间表。注意第三只海鸥在岛上跨年停留。 :::align{center}  图 C.1. 样例输出 1 中海鸥的访问时间表 ::: 翻译由 DeepSeek V3 完成