P14684 [ICPC 2025 Yokohama R] Cutting Tofu

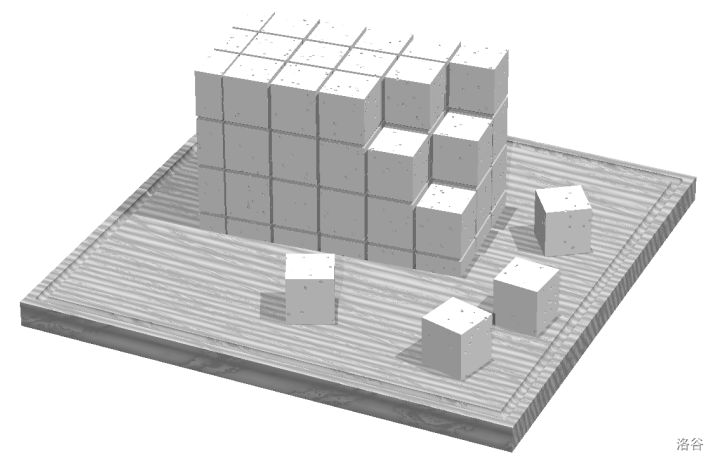
你正在准备日本人最喜爱的味增汤，并使用了最受欢迎的食材之一——**豆腐**。豆腐是一种白色的长方体状食物，通常被切成小块后再放入汤中。 你计划切一块豆腐块，以制作至少所需数量的、大小相同的豆腐立方块。你沿着平行于豆腐块各面的平面进行切割。每一次切割都贯穿整个豆腐块，并将经过的所有部分分开。在豆腐立方块被完全切出之前，你不能移动豆腐块或其碎片。 :::align{center}  图 E.1. 一个切割豆腐的示例 ::: 只要能够得到所需数量的豆腐立方块，你希望立方块尽可能大。你并不介意有多余的豆腐立方块或边角料，因为它们可以用于制作其他菜肴。 给定豆腐块的长、宽、高（以单位长度的整数倍表示）以及所需的豆腐立方块数量，你的任务是找出豆腐立方块可能的最大边长。可以证明，在给定的约束条件下，答案是一个有理数，因此应表示为最简分数形式。

输入包含一个或多个测试用例。输入的第一行包含一个整数 $t$ ($1 \le t \le 10^4$)，表示测试用例的数量。接下来是 $t$ 个测试用例的描述，每个用例的格式如下。 $$ a\ b\ c $$ $$ k $$ 三个整数 $a$、$b$ 和 $c$ 分别表示豆腐块的长、宽、高。它们都在 $1$ 到 $10^9$ 之间（含）。整数 $k$ ($1 \le k \le 10^9$) 表示所需的豆腐立方块数量。

对于每个测试用例，输出一行两个正整数 $p$ 和 $q$，用一个空格分隔。这里 $p$ 和 $q$ 互质，即 $p/q$ 是豆腐立方块可能的最大边长。

翻译由 DeepSeek V3 完成