P14685 [ICPC 2025 Yokohama R] Astral Geometry
题目描述
作为一名年轻的天文学家,你对一组具有独特特征的恒星的空间排列很感兴趣。了解这一点可能有助于理解早期宇宙的宇宙学。为此,你可以使用一种专门的仪器进行测量。
该仪器使用其自身的三维笛卡尔坐标系,其中原点 $(0, 0, 0)$ 设在地球上,恒星的位置被建模为格点(所有坐标均为整数的点)。你已经知道所有感兴趣的恒星到地球的距离,但它们的方向未知。
在一次测量中,你指定两颗不同的恒星,仪器会报告它们之间的距离。请注意,仪器不会报告恒星的绝对或相对方向。
请在有限的测量次数内确定所有恒星对之间的距离。
**交互**
输入的第一行包含一个整数 $n$,表示感兴趣的恒星数量 ($2 \le n \le 100$)。恒星编号为 $1$ 到 $n$。第二行包含 $n$ 个整数。其中第 $i$ 个是恒星 $i$ 到原点的**距离平方**。保证所有恒星都有整数坐标,每个坐标在 $-4000$ 到 $4000$ 之间(含)。没有两颗恒星在同一位置。没有恒星位于原点。
读取这两行后,你可以开始测量。要测量恒星 $i$ 和 $j$ 之间的距离,请输出一行 "measure $i$ $j$",其中 $i$ 和 $j$ 是 $1$ 到 $n$(含)之间的不同整数。作为响应,将有一行输入可用,其中包含一个表示恒星 $i$ 和 $j$ 之间距离平方的整数。你最多可以进行 $300$ 次测量。
当你确定了所有恒星对之间的距离后,请输出一行仅包含 **answer** 的行,然后按以下格式输出 $n-1$ 行。
$$
d_{1,2}\ d_{1,3}\ \cdots\ d_{1,n}
$$
$$
d_{2,3}\ \cdots\ d_{2,n}
$$
$$
\vdots
$$
$$
d_{n-1,n}
$$
这里,$d_{i,j}$ ($1 \le i < j \le n$) 是一个整数,表示恒星 $i$ 和 $j$ 之间的距离平方。请注意,你不需要确定恒星的坐标。输出这些行后,交互停止,你的程序必须终止,不再输出任何额外内容。
如果你的输出不符合上述规范,或者测量次数超过 $300$,你的提交将被判为错误答案。
恒星的坐标在交互开始前就已固定;交互期间不会改变。
~~我们提供了一个命令行工具供本地测试。更多详情,请参阅竞赛系统中的澄清说明。~~
输入格式
无
输出格式
无
说明/提示
在样例交互 1 中,恒星的坐标可以如下:
- 恒星 1 位于 $(1, 0, 0)$,
- 恒星 2 位于 $(-1, -1, 3)$,
- 恒星 3 位于 $(-2, 0, 0)$。
恒星 1 和 2 之间的距离是 $\sqrt{14}$。在第一次测量中,返回了距离平方 $14$。
:::align{center}
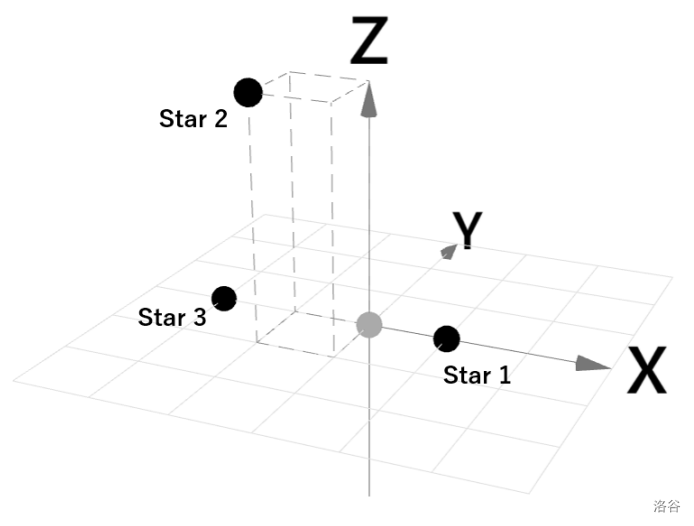
图 F.1. 样例交互 1 图示
:::
在样例交互 2 中,恒星的坐标可以如下:
- 恒星 1 位于 $(-3998, -3998, -3997)$,
- 恒星 2 位于 $(3997, 3997, 3996)$,
- 恒星 3 位于 $(-3999, -3998, -3998)$,
- 恒星 4 位于 $(3999, 3999, 3998)$。
在样例交互 3 中,恒星的坐标可以如下:
- 恒星 1 位于 $(1, 0, 0)$,
- 恒星 2 位于 $(0, -2, 0)$,
- 恒星 3 位于 $(0, 0, 3)$,
- 恒星 4 位于 $(3, -4, 5)$,
- 恒星 5 位于 $(-6, 7, -8)$。
翻译由 DeepSeek V3 完成