P14691 [ICPC 2025 Yokohama R] Common Tangent Lines

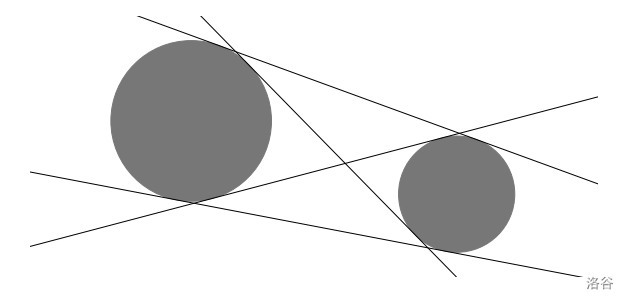
众所周知，平面上两个不相交（既不重叠也不相切）的圆有 **四条不同的公切线**。 :::align{center}  ::: 给定 $xy$ 平面上的四条直线。你的目标是：对这些直线施加**平行移动**，使得它们成为**某对半径为正且不相交的圆**的四条不同的公切线。你希望以尽可能低的 **成本** 完成此操作，其中成本定义为平移距离的总和。一条直线的平移距离是其平移前后两直线之间的距离。 每条直线由两个参数 $a$ 和 $d$ 指定，并由以下方程定义： $$ x \cos\left(\frac{\pi a}{180}\right) + y \sin\left(\frac{\pi a}{180}\right) = d. $$ 例如，参数为 $(a, d) = (60, 1)$ 的直线代表 $x/2 + \sqrt{3}y/2 = 1$，因为 $\cos(\pi/3) = 1/2$ 且 $\sin(\pi/3) = \sqrt{3}/2$。 首先，判断目标是否可达。如果可达，确定 **最小所需成本**，其定义如下：最小的值 $c$，使得对于任意正实数 $\varepsilon$，都能以不超过 $c + \varepsilon$ 的成本实现目标。目标不必以恰好等于 $c$ 的成本实现。

输入包含一个或多个测试用例。输入的第一行包含一个整数 $t$ ($1 \le t \le 1000$)，表示测试用例的数量。接下来是 $t$ 个测试用例的描述，每个用例的格式如下。 $$ a_1\ d_1 $$ $$ \vdots $$ $$ a_4\ d_4 $$ 对于 $i = 1, \ldots, 4$，两个整数 $a_i$ 和 $d_i$ 是用于指定第 $i$ 条直线的参数 ($0 \le a_i < 180$， $-1000 \le d_i \le 1000$)。在平移之前，两条或多条直线可能相同。

对于每个测试用例，如果目标不可达，则输出一行 $no$。否则，输出一行上述定义的最小所需成本。输出的绝对或相对误差必须小于等于 $10^{-7}$。

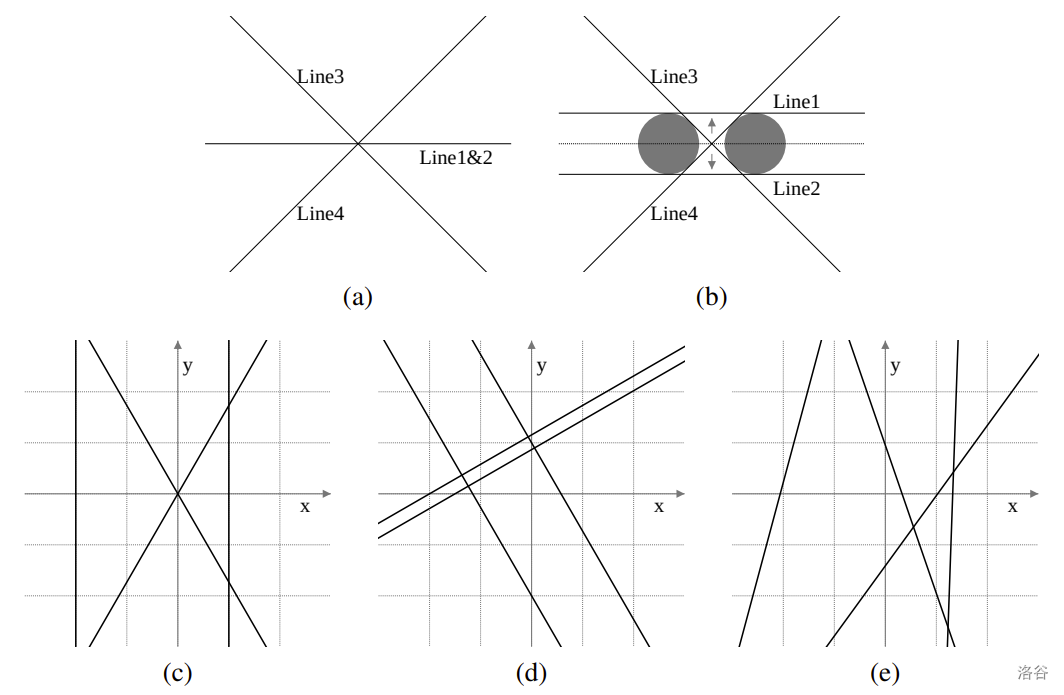
在样例输入 1 的第一个测试用例中，你至少需要移动前两条相同的直线之一（图 L.1 (a)）。对于任意 $\varepsilon > 0$，将其中一条直线沿 $y$ 轴正方向平移 $\varepsilon/2$，另一条沿 $y$ 轴负方向平移 $\varepsilon/2$，即可在成本为 $\varepsilon$ 的情况下实现目标。这将产生半径为 $\varepsilon/2$ 的圆的四条公切线（图 L.1 (b)）。由于 $\varepsilon$ 可以任意小，最小所需成本为 $0$。其余情况如图 L.1 (c) 至 (e) 所示。 :::align{center}  图 L.1. 样例输入 1 图示 ::: 翻译由 DeepSeek V3 完成