P14707 [ICPC 2023 Tehran R] Largest Triangle
Description
A "terrain" is an $x$-monotone polygon defined by the points $p_1, \ldots, p_n$ where each point $p_i$ has coordinates $(x_i, y_i)$, and the following three conditions hold:
- $y_1 = y_n = 0$
- $y_i > 0$ for $1 < i < n$
- $x_i < x_{i+1}$ for $1 \leq i < n$
Given a terrain defined by the points $p_1, \ldots, p_n$, find the largest triangle that fits entirely within the terrain, and one of its three vertices is positioned at one of the terrain points $p_2$ through $p_{n-1}$.
:::align{center}
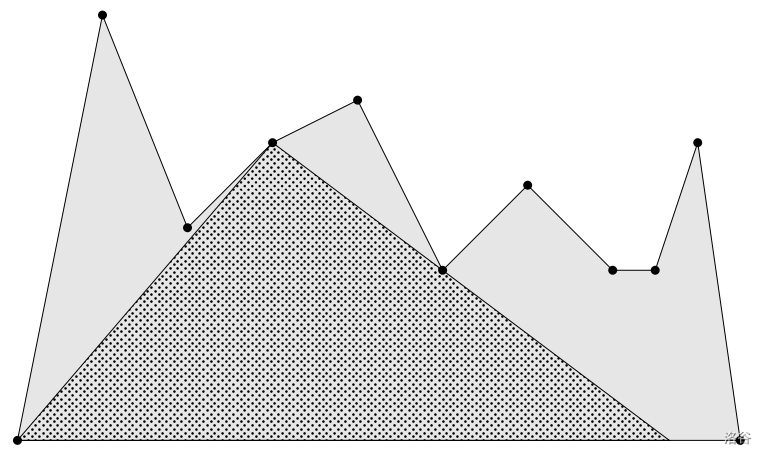
:::
Input Format
The first line of input contains an integer $n$, representing the number of points in the terrain ($3 \leq n \leq 10^5$). The $i^{th}$ line in the following $n$ lines consists of two space-separated integers $x_i$ and $y_i$, representing the point $p_i$ of the terrain ($0 \leq x_i, y_i \leq 10^9$).
Output Format
Print the area of the largest triangle contained within the terrain. Your output will be considered correct if its absolute or relative error is at most $10^{-6}$.