P14716 [RMI 2025] 电缆维护 / Engineers

由于官方未提供时限和空限，将 TL 设置为 std 的两倍，ML 设置为 2G。

给定一棵 $N$ 个点的树，点编号 $0\sim N-1$。点 $i$ 有正整数点权 $C_i$。 给定正整数 $D$。构造若干条**简单**路径（点集可以有交），使得未被路径覆盖的点的点权差值不大于 $D$。 形式化地说，设未被覆盖的点集为 $R$，你需要保证 $\forall i,j\in R$，都有 $|C_i-C_j|\le D$。 在满足上述条件的前提下最小化路径数量。只需要求出路径数量。 ### 实现细节 这是一道（函数式）交互题。你不需要，也不应该定义 `main` 函数。 你需要实现函数 ```cpp int solve(int N, int D, std::vector C, std::vector P, std::vector Q) ``` 该函数接收以下参数： - 点数 $N$； - 最大可接受差值 $D$； - 点权 $C$； - 两个长度为 $N-1$ 的 `vector` $P$ 和 $Q$，表示对所有 $0 \le i \le N-1$，存在树边 $(P_i,Q_i)$。 返回符合条件的路径的最少数量。

见「实现细节」。

见「实现细节」。

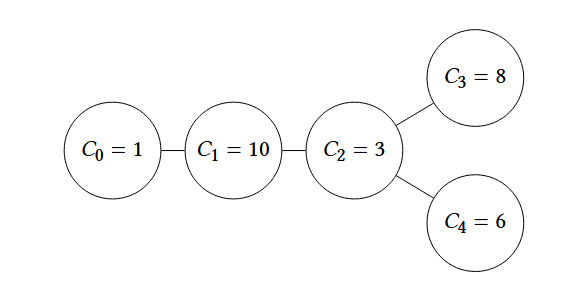
### 样例解释 在样例一中，有 $N=5$ 且 $D=3$。树的结构如图所示： ::::align{center}  :::: 一种合法的方案为构造路径 $[0,1,2,3]$。 ### 限制条件 * $1 \le N \le 200\,000$。 * 对所有 $0 \le i \le N-1$ ，有 $1 \le C_i \le 1\,000\,000\,000$。 * $1 \le D \le 1\,000\,000\,000$。 * $0 \le p_i, q_i < N$ ，$p_i \ne q_i$，且 $(p_i, q_i)$ 互不相同。 ### 子任务 | # | 分值 | 约束 | |:---:|:---:|:---| | $1$ | $7 $ | $N \le 20$ 且对所有 $0 \le i \le N-1$ ，有 $1 \le C_i \le 50$。 | | $2$ | $6 $ | $N \le 1000$ 且对所有 $0 \le i \le N-1$ ，有 $1 \le C_i \le 1000$。 | | $3$ | $11$ | $N \le 1000$。 | | $4$ | $16$ | 对所有 $0 \le i < N-1$ ，有 $p_i = 0, q_i = i+1$。 | | $5$ | $26$ | $N \le 50000$。 | | $6$ | $34$ | 无额外约束。 |