P14717 [RMI 2025] 猜排列 / Guess Permutation
题目背景
**不要引入头文件**。在文件头粘贴
```cpp
#include
int press_button(int);
```
以评测。
题目描述
**这是一道交互题。本题中,交互库是非自适应的。**
有一台破旧的机器,有 $N$ 个**隐藏的**开关,编号 $0\sim N-1$。开关的状态用 $s_0,\ldots,s_{N-1}$ 来表示。我们说开关 $i$ **断开**,当且仅当 $s_i=0$;否则 $s_i=1$,开关 $i$ **接通**。
起初,所有开关都是断开的。
有 $N$ 个按钮,编号 $0\sim N-1$。有一个**隐藏的** $0\sim N-1$ 的排列,记为 $P=[p_0,\ldots,p_{N-1}]$。
现在想要确定 $P$。为此,你可以进行如下的操作:
> **操作**
>
> - 选定 $i$ 满足 $0\le i\lt n$,按下按钮 $i$。
> - 令本次操作**前**(不含本次)一共进行了 $k$ 次操作。
> - 翻转开关 $p_{k\bmod N}$ 的状态。形式化地,令 $s_{p_{k\bmod N}}\gets 1-s_{p_{k\bmod N}}$。
> - 你将得知 $s_i$ 的值。
给定 $N$,你需要用至多 $50N$ 次操作找出排列 $P$。
为了获得满分,需要更少的操作次数,详见「计分方式」。
### 实现细节
**这是一道(函数式)交互题。你不需要,也不应该定义 `main` 函数。**
你需要实现函数
```cpp
std::vector solve(int N);
```
该函数接收参数 $N$;返回长度为 $N$ 的 `vector` $q$ 满足 $q[i]=p[i]$。该函数每个测试点仅调用一次。
你可以调用以下的函数:
```cpp
int press_button(int i);
```
描述一次按下按钮 $i$ 的操作,返回操作后 $s_i$ 的值。
### Sample Grader
在附件中附有 sample grader($\texttt{sample-grader.cpp}$)。其输入格式如下:
- 第一行:正整数 $N$
- 第二行:$N$ 个整数 $p_0,p_1,\ldots,p_{N-1}$。
它会调用 `solve(N)` 函数,报告你程序的运行结果:若通过,输出查询次数;否则,输出错误信息。
输入格式
见「实现细节」。
输出格式
见「实现细节」。
说明/提示
### 样例解释
考虑 $N=4,P=[1,3,0,2]$ 和以下的调用。
| 操作 | $S=$ | 返回值 |
|------------------|-------|--------------|
| $\texttt{press\_button(0)}$ | $\texttt{0100}$ | $\texttt{ }$ |
| $\texttt{press\_button(1)}$ | $\texttt{0101}$ | $\texttt{0}$ |
| $\texttt{press\_button(2)}$ | $\texttt{1101}$ | $\texttt{1}$ |
| $\texttt{press\_button(3)}$ | $\texttt{1111}$ | $\texttt{0}$ |
| $\texttt{press\_button(1)}$ | $\texttt{1011}$ | $\texttt{1}$ |
| $\texttt{press\_button(3)}$ | $\texttt{1010}$ | $\texttt{0}$ |
| $\texttt{press\_button(2)}$ | $\texttt{0010}$ | $\texttt{0}$ |
| 返回 $\texttt{\{1,3,0,2\}}$ | | $\texttt{1}$ |
### 限制条件
- $N\le 10^4$。
- $P$ 是 $0\sim N-1$ 的排列。
### 子任务
| # | 得分 | $N=$ |
| :-: | :-: | :-: |
| $1$ | $20$ | $32$ |
| $2$ | $40$ | $1\, 000$ |
| $3$ | $40$ | $10\, 000$ |
### 计分方式
如果你的程序未能成功结束,或者答案错误,得 $0$ 分。
否则,令 $K$ 为你的程序调用 `press_button()` 的次数。令 $Q=K/N$,若 $Q>50$,得 $0$ 分。否则,每个子任务得分为系数 $S$ 乘以子任务满分。$S$ 的计算方式如下:
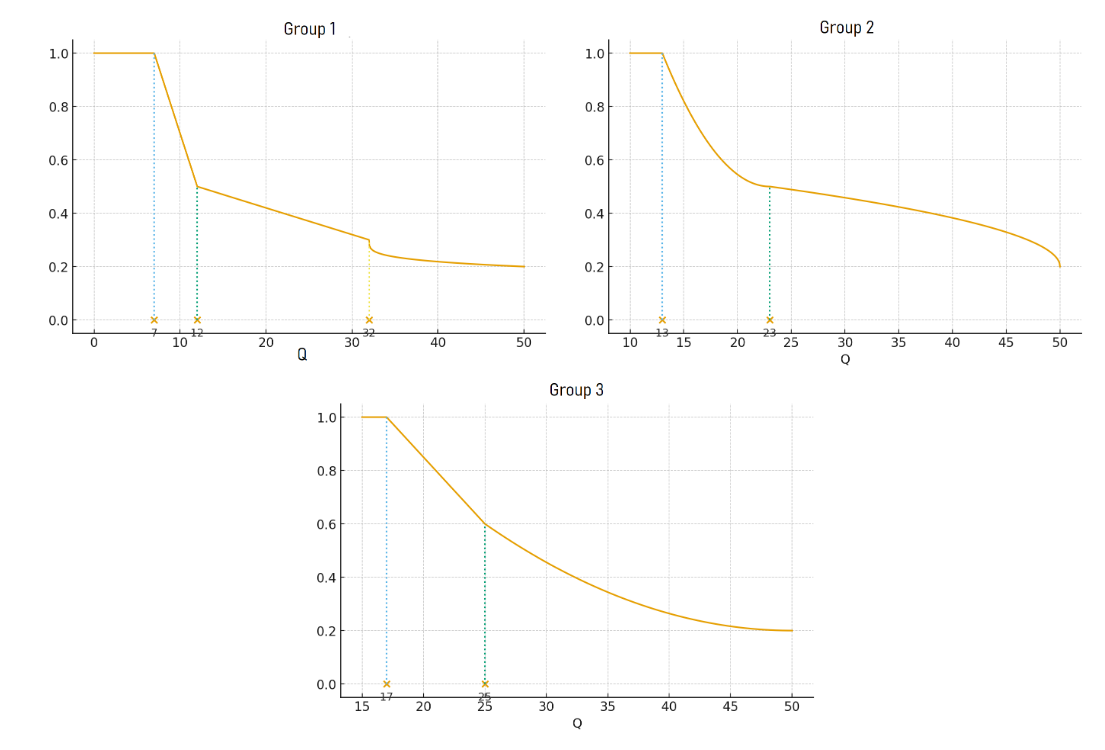
- 子任务 $1$:$\displaystyle S=\begin{cases} \displaystyle 1, & Q\le 7 \\ \displaystyle 1-\frac{1}{10}(Q-7), & 7\lt Q\le 12 \\ \displaystyle \frac{1}{2}-\frac{1}{100}(Q-12), & 12\lt Q\le 32 \\ \displaystyle \frac{3}{10}-\frac{1}{10}\sqrt[4]{\frac{Q-32}{18}}, & 32\lt Q\le 50\end{cases}$
- 子任务 $2$:$\displaystyle S=\begin{cases} \displaystyle 1, & Q\le 13 \\ \displaystyle \frac{1}{2}+\frac{1}{2}\left(\frac{23-Q}{10}\right)^2, & 13\lt Q\le 23 \\ \displaystyle \frac{1}{5}+\frac{3}{10}\sqrt{\frac{50-Q}{27}}, & 23\lt Q\le 50\end{cases}$
- 子任务 $3$:$\displaystyle S=\begin{cases} \displaystyle 1, & Q\le 17 \\ \displaystyle \frac{3}{5}+\frac{25-Q}{20}, & 17\lt Q\le 25 \\ \displaystyle \frac{1}{5}+\frac{2}{5}\left(\frac{50-Q}{25}\right)^2, & 25\lt Q\le 50\end{cases}$
你可以利用下图获得直观感受。
::::align{center}
::::